ガラパゴ三角関数

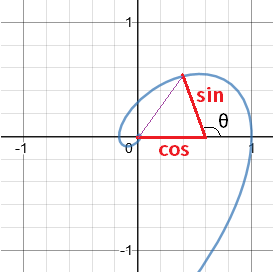
ガラパゴ三角関数（ガラパゴさんかくかんすう）とは、$$+1$$ と $$z=e^{i\theta}$$ を理論上の基底の元（$$z$$ が実数であっても独立した元であるものとみなして区別）とする斜交座標系において、極座標 $$e^{xz}$$ が示す座標の実部と $$z$$ 部を得る関数である。一般的な三角関数の純粋な拡張として みゆ により考案された。

目次

概要

ガラパゴ三角関数 $$\cos_zx$$、$$\sin_zx$$ は、次のように表される。

$$\begin{align*} &\lim_{n\to\infty}\left(1+\frac{x}{n}z\right)^n=e^{xz}=\cos_zx+z\sin_zx\\ &\quad\begin{cases} z=e^{i\theta}\\ \displaystyle\cos_zx=\lim_{t\to\theta}\left[e^{x\cos t}\cos(x\sin t)-\frac{e^{x\cos t}\sin(x\sin t)}{\tan t}\right]\\ \displaystyle\sin_zx=\lim_{t\to\theta}\left[\frac{e^{x\cos t}\sin(x\sin t)}{\sin t}\right] \end{cases} \end{align*}$$

この式は次の数列

$$\begin{pmatrix}A_{n+1}\\A_n\end{pmatrix}=\begin{pmatrix}2\cos\theta&-1\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix}$$ すなわち $$\begin{cases} A_0=0\\ A_1=1\\ A_{n}=(2\cos\theta)A_{n-1}-A_{n-2} \end{cases}$$

を用いると、級数展開型にて書き改めることができる。

$$\begin{align*} e^{xz}=&\cos_zx+z\sin_zx\\ =&\left(-\sum_{k=0}^\infty\frac{A_{k-1}x^k}{k!}\right)+z\left(\sum_{k=0}^\infty\frac{A_{k}x^k}{k!}\right)\\ \end{align*}$$

$$z=e^{i\theta}=\cos\theta+i\sin\theta$$、すなわち $$e^{xz}=e^{x(\cos\theta+i\sin\theta)}=e^{x\cos\theta+ix\sin\theta}$$ であることから、

$$e^{xz}$$ の偏角は $$\arg e^{xz}=x\sin\theta$$、絶対値は $$|e^{xz}|=e^{x\cos\theta}$$ であることがわかる。

$$\{\theta\ne N\pi\mid N\in\mathbb{Z}\}$$ においては $$|e^{xz}|=1$$ へ標準化することで直交座標系との関係性が次のように示される。

$$\begin{cases} \alpha=\arg e^{xz}=x\sin\theta\\ \begin{align*} e^{i\alpha}=&\cos\alpha+i\sin\alpha\\ =&e^{-\alpha\cot\theta}\left[\cos_z\frac{\alpha}{\sin\theta}+z\sin_z\frac{\alpha}{\sin\theta}\right]\end{align*} \end{cases}$$

導出

$$z=e^{i\theta}$$ において、 $$e^{xz}=\cos_zx+z\sin_zx$$ の両辺を直交座標形式に変換

左辺

$$\begin{align*} e^{xz}=&e^{xe^{i\theta}}\\ =&e^{x(\cos\theta+i\sin\theta)}\\ =&e^{x\cos\theta}\cdot e^{ix\sin\theta}\\ =&e^{x\cos\theta}[\cos(x\sin\theta)+i\sin(x\sin\theta)]\\ =&e^{x\cos\theta}\cos(x\sin\theta)+ie^{x\cos\theta}\sin(x\sin\theta) \end{align*}$$

右辺

$$\begin{align*} &\cos_zx+z\sin_zx\\ =&\cos_zx+(\cos\theta+i\sin\theta)\sin_zx\\ =&\left[\cos_zx+\cos\theta\sin_zx\right]+i\sin\theta\sin_zx \end{align*}$$

両辺の実部と虚部をそれぞれ比較

$$e^{x\cos\theta}\cos(x\sin\theta)=\cos_zx+\cos\theta\sin_zx$$

$$e^{x\cos\theta}\sin(x\sin\theta)=\sin\theta\sin_zx$$

$$\theta$$ が $$\pi$$ の整数倍の場合、 $$1$$ と $$e^{i\theta}$$ は線形従属となってしまうため、$$\theta$$ を $$t$$ とおいて $$t\to\theta$$ の極限として考える

$$\begin{align*} \cos_zx&=\lim_{t\to\theta}\left[e^{x\cos t}\cos(x\sin t)-\frac{e^{x\cos t}\sin(x\sin t)}{\tan t}\right]\\ \sin_zx&=\lim_{t\to\theta}\left[\frac{e^{x\cos t}\sin(x\sin t)}{\sin t}\right]\\ \end{align*}$$

級数展開形

$$+1$$ と $$z=e^{i\theta}$$ を（理論上の）基底の元とする斜交座標形式の複素数平面において、関数 $$f(x)=e^{xz}$$ を想定する。

$$\exp$$関数のマクローリン展開より

$$\begin{align*} e^{xz}=&\exp(xz)\\ =&\sum_{n=0}^{\infty}\frac{(xz)^n}{n!}\\ =&\frac{(xz)^0}{0!}+\frac{(xz)^1}{1!}+\sum_{n=2}^\infty\frac{(xz)^n}{n!}\\ =&1+xz+\sum_{n=2}^\infty\frac{x^n}{n!}z^n\\ \end{align*}$$

ガラパゴ累乗定理により $$z^n$$ は $$+1$$ 成分 と $$+z$$ 成分に分離できるため

$$\displaystyle\cos_zx=1-\sum_{n=2}^\infty\frac{x^n}{n!}\left[\sum_{k=0}^{\lfloor (n-2)/2\rfloor}\binom{n-k-2}{k}(-1)^k\left(2\cos\theta\right)^{n-2k-2}\right]$$

$$\displaystyle\sin_zx=x+\sum_{n=2}^\infty\frac{x^n}{n!}\left[\sum_{k=0}^{\lfloor (n-1)/2\rfloor}\binom{n-k-1}{k}(-1)^k\left(2\cos\theta\right)^{n-2k-1}\right]$$

あるいは漸化式を用いて

$$\begin{align*} \cos_zx=&-\sum_{k=0}^\infty\frac{A_{k-1}x^k}{k!}\\ \sin_zx=&+\sum_{k=0}^\infty\frac{A_{k}x^k}{k!}\\ \end{align*} \begin{cases} A_0=0\\ A_1=1\\ A_{k}=(2\cos\theta)A_{k-1}-A_{k-2} \end{cases} $$

$$z=\mathrm{P}=e^{2\pi i}=1$$ のとき $$\rightarrow~2\cos\theta=2$$

$$\displaystyle\cos_zx=(1-x)e^x$$

$$\displaystyle\sin_zx=xe^x$$

$$z=\mathrm{P}^\frac12=e^{\frac{1}{2}\cdotp2\pi i}=-1$$（$$1$$ の原始 $$2$$ 乗根）のとき $$\rightarrow~2\cos\theta=-2$$

$$\displaystyle\cos_zx=(1+x)e^{-x}$$

$$\displaystyle\sin_zx=xe^{-x}$$

$$z=\mathrm{P}^\frac13=e^{\frac{1}{3}\cdotp2\pi i}$$（$$1$$ の原始 $$3$$ 乗根）のとき $$\rightarrow~2\cos\theta=-1$$

$$\displaystyle\cos_zx=\sum_{k=0}^{\infty}\frac{x^{3k}}{(3k)!}-\sum_{k=0}^{\infty}\frac{x^{3k+2}}{(3k+2)!}$$

$$\displaystyle\sin_zx=\sum_{k=0}^{\infty}\frac{x^{3k+1}}{(3k+1)!}-\sum_{k=0}^{\infty}\frac{x^{3k+2}}{(3k+2)!}$$

$$z=\mathrm{P}^\frac14=e^{\frac{1}{4}\cdotp2\pi i}$$（$$1$$ の原始 $$4$$ 乗根）のとき $$\rightarrow~2\cos\theta=0$$

$$\displaystyle\cos_zx=\sum_{k=0}^{\infty}\frac{x^{4k}}{(4k)!}-\sum_{k=0}^{\infty}\frac{x^{4k+2}}{(4k+2)!}=\cos x$$

$$\displaystyle\sin_zx=\sum_{k=0}^{\infty}\frac{x^{4k+1}}{(4k+1)!}-\sum_{k=0}^{\infty}\frac{x^{4k+3}}{(4k+3)!}=\sin x$$

exps関数を用いた表現

$$\mathrm{exp}_s$$ 関数（skipped exponential 関数）を次のように定義する。

$$\displaystyle\exp_s(x)=\left(\sum_{k=0}^\infty\frac{x^{ks}}{(ks)!}\right)$$

この関数は $$\exp$$ 関数をマクローリン展開した各項のうち、$$x$$ の指数が $$s$$ の倍数である項のみによって構成される関数であり、$$s$$ 階微分することで元の関数と一致する（周階導関数）。

この関数を $$m$$ 階微分すると

$$\begin{align*} \mathrm{exps}^{(m)}_s(x) =&\frac{1}{s}\sum_{k=0}^\infty\left[\left(e^{\frac{m}{s}\cdot2\pi i}\right)^ke^{\left(e^{\frac{2\pi i}{s}}\right)^kx}\right]\\ =&\frac{1}{s}\sum_{k=0}^\infty\left[\exp\left(\frac{2km\pi}{s}i+\exp\left(\frac{2k\pi}{s}i\right)x\right)\right] \end{align*}$$

と表されるが、マクローリン展開形を考えれば単に各項の次数が落ちるだけと見ることができる。

すなわち、$$m=0$$ から $$m=s-1$$ までの $$s$$ 種類の関数を標準基底の元とすることで、あらゆる $$s$$ 階の周階導関数を構成可能である。

ガラパゴ三角関数は $$z=e^{i\theta}$$ が実数ではなく、かつ、$$\frac{\theta}{2\pi}$$ が有理数のときに周階導関数となるため、$$\mathrm{exp}_s$$ 関数の $$m$$ 階導関数を用いて以下のように示すことが可能である。

$$z=\mathrm{P}^{\frac13}=e^{\frac{2\pi}3i}$$ の場合 \begin{array}{c} +\cos_{z}x && &=& \exp_3^{(0)}x-\exp_3^{(1)}x &\leftarrow[+1,~~0~,-1]\\ -\sin_{z}x &=& +\sin_{z^{-1}}x &=& \exp_3^{(1)}x-\exp_3^{(2)}x &\leftarrow[~~0~,-1,+1]\\ && -\cos_{z^{-1}}x &=& \exp_3^{(2)}x-\exp_3^{(0)}x &\leftarrow[-1,+1,~~0~]\\ \\ -\cos_{z}x && &=& -\exp_3^{(0)}x+\exp_3^{(1)}x &\leftarrow[-1,~~0~,+1]\\ +\sin_{z}x &=& -\sin_{z^{-1}}x &=& -\exp_3^{(1)}x+\exp_3^{(2)}x &\leftarrow[~~0~,+1,-1]\\ && +\cos_{z^{-1}}x &=& -\exp_3^{(2)}x+\exp_3^{(0)}x &\leftarrow[+1,-1,~~0~]\\ \end{array}

$$z=\mathrm{P}^{\frac14}=e^{\frac{2\pi}4i}=e^{\frac{\pi}2i}$$ の場合 \begin{array}{c} +\cos x &=& +\cos_zx &=& +\cos_{z^{-1}}x &=& \exp_4^{(0)}x-\exp_4^{(2)}x &\leftarrow[+1,~~0~,-1,~~0~]\\ -\sin x &=& -\sin_zx &=& +\sin_{z^{-1}}x &=& \exp_4^{(1)}x-\exp_4^{(3)}x &\leftarrow[~~0~,-1,~~0~,+1]\\ -\cos x &=& -\cos_zx &=& -\cos_{z^{-1}}x &=& \exp_4^{(2)}x-\exp_4^{(0)}x &\leftarrow[-1,~~0~,+1,~~0~]\\ +\sin x &=& +\sin_zx &=& -\sin_{z^{-1}}x &=& \exp_4^{(3)}x-\exp_4^{(1)}x &\leftarrow[~~0~,+1,~~0~,-1]\\ \end{array}

$$z=\mathrm{P}^{\frac15}=e^{\frac{2\pi}5i}$$ の場合（$$\phi'=\phi-1=\frac{\sqrt5-1}2$$） \begin{array}{c} +\cos_zx && &=& +\exp_5^{(0)}x-\exp_4^{(3)}x-\phi'\exp_4^{(2)}x+\phi'\exp_4^{(1)}x &\leftarrow[+1~,~~0~~,-1~,-\phi',+\phi']\\ -\sin_zx &=& +\sin_{z^{-1}}x &=& +\exp_5^{(1)}x-\exp_4^{(4)}x-\phi'\exp_4^{(3)}x+\phi'\exp_4^{(2)}x &\leftarrow[~~0~~,-1~,-\phi',+\phi',+1~]\\ && -\cos_{z^{-1}}x &=& +\exp_5^{(2)}x-\exp_4^{(5)}x-\phi'\exp_4^{(4)}x+\phi'\exp_4^{(3)}x &\leftarrow[-1~,-\phi',+\phi',+1~,~~0~~]\\ && (+\sin_{z^{-1}}x)'' &=& +\exp_5^{(3)}x-\exp_4^{(0)}x-\phi'\exp_4^{(5)}x+\phi'\exp_4^{(4)}x &\leftarrow[-\phi',+\phi',+1~,~~0~~,-1~]\\ && (-\cos_{z^{-1}}x)'' &=& +\exp_5^{(4)}x-\exp_4^{(1)}x-\phi'\exp_4^{(0)}x+\phi'\exp_4^{(5)}x &\leftarrow[+\phi',+1~,~~0~~,-1~,-\phi']\\ \\ -\cos_zx && &=& -\exp_5^{(0)}x+\exp_4^{(3)}x+\phi'\exp_4^{(2)}x-\phi'\exp_4^{(1)}x &\leftarrow[-1~,~~0~~,+1~,+\phi',-\phi']\\ +\sin_zx &=& -\sin_{z^{-1}}x &=& -\exp_5^{(1)}x+\exp_4^{(4)}x+\phi'\exp_4^{(3)}x-\phi'\exp_4^{(2)}x &\leftarrow[~~0~~,+1~,+\phi',-\phi',-1~]\\ && +\cos_{z^{-1}}x &=& -\exp_5^{(2)}x+\exp_4^{(0)}x+\phi'\exp_4^{(4)}x-\phi'\exp_4^{(3)}x &\leftarrow[+1~,+\phi',-\phi',-1~,~~0~~]\\ && (-\sin_{z^{-1}}x)'' &=& -\exp_5^{(3)}x+\exp_4^{(1)}x+\phi'\exp_4^{(0)}x-\phi'\exp_4^{(4)}x &\leftarrow[+\phi',-\phi',-1~,~~0~~,+1~]\\ && (+\cos_{z^{-1}}x)'' &=& -\exp_5^{(4)}x+\exp_4^{(2)}x+\phi'\exp_4^{(1)}x-\phi'\exp_4^{(0)}x &\leftarrow[-\phi',-1~,~~0~~,+1~,+\phi']\\ \end{array}

$$z=\mathrm{P}^{\frac16}=e^{\frac{2\pi}6i}=e^{\frac{\pi}3i}$$ の場合 \begin{array}{c} +\cos_{z}x && &=& \exp_6^{(0)}x-\exp_6^{(4)}x-\exp_6^{(3)}x+\exp_6^{(1)}x &\leftarrow[+1,~~0~,-1,-1,~~0~,+1]\\ -\sin_{z}x &=& +\sin_{z^{-1}}x &=& \exp_6^{(1)}x-\exp_6^{(5)}x-\exp_6^{(4)}x+\exp_6^{(2)}x &\leftarrow[~~0~,-1,-1,~~0~,+1,+1]\\ && -\cos_{z^{-1}}x &=& \exp_6^{(2)}x-\exp_6^{(0)}x-\exp_6^{(5)}x+\exp_6^{(3)}x &\leftarrow[-1,-1,~~0~,+1,+1,~~0~]\\ -\cos_{z}x && &=& \exp_6^{(3)}x-\exp_6^{(1)}x-\exp_6^{(0)}x+\exp_6^{(4)}x &\leftarrow[-1,~~0~,+1,+1,~~0~,-1]\\ +\sin_{z}x &=& -\sin_{z^{-1}}x &=& \exp_6^{(4)}x-\exp_6^{(2)}x-\exp_6^{(1)}x+\exp_6^{(5)}x &\leftarrow[~~0~,+1,+1,~~0~,-1,-1]\\ && +\cos_{z^{-1}}x &=& \exp_6^{(5)}x-\exp_6^{(3)}x-\exp_6^{(2)}x+\exp_6^{(0)}x &\leftarrow[+1,+1,~~0~,-1,-1,~~0~]\\ \end{array}