「ガラパゴ累乗定理」の版間の差分
| (3人の利用者による、間の40版が非表示) | |||
| 1行目: | 1行目: | ||
| − | '''ガラパゴ累乗定理'''(ガラパゴるいじょうていり)とは、複素数 $$z$$ の累乗は $$ | + | '''ガラパゴ累乗定理'''(ガラパゴるいじょうていり)とは、複素数 $$z$$ の累乗は $$z+\overline{z}$$ と $$z\cdot\overline{z}$$ を元とする多項式より生成される実数を係数とする $$z$$ の一次式で表せるという定理である。 |
[[ガラパゴ数学]]の主定理の一つで、$$+1$$ と $$+z$$ を基底の元とする $$\mathbb{R}^2$$ 斜交平面上の幾何を扱うことを主目的として [[みゆ]] によって導出された。 | [[ガラパゴ数学]]の主定理の一つで、$$+1$$ と $$+z$$ を基底の元とする $$\mathbb{R}^2$$ 斜交平面上の幾何を扱うことを主目的として [[みゆ]] によって導出された。 | ||
[[ファイル:実数1と複素数Zを基底の元とするR².png |480px|center|border|実数1と複素数Zを基底の元とするR²のイメージ]] | [[ファイル:実数1と複素数Zを基底の元とするR².png |480px|center|border|実数1と複素数Zを基底の元とするR²のイメージ]] | ||
| + | |||
== 概要 == | == 概要 == | ||
| − | 複素数 $$z$$ の 整数 $$n$$ 乗は、$$ | + | 複素数 $$z$$ の 整数 $$n$$ 乗は、$$l=z\cdotp\bar{z}=|z|^2$$ と $$r=z+\bar{z}=2\mathrm{Re}(z)$$ を用いて次のように表せる。 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:$$\begin{array}{l} | :$$\begin{array}{l} | ||
| − | z^1=&z\\ | + | \begin{pmatrix} |
| − | z^2=& | + | z^n\\z^{n+1}\end{pmatrix}&=\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}\begin{pmatrix}1\\z\end{pmatrix}\\ |
| − | z^3=&(r^2 | + | &=\begin{pmatrix}0&1\\-l&r\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix}=\begin{pmatrix}0&1\\-z\cdotp\bar{z}&z+\bar{z}\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix} |
| − | z^4=&(r^ | + | \end{array}$$ |
| − | z^5=&(r^ | + | |
| + | |||
| + | ここで得られる数列 | ||
| + | |||
| + | :$$\begin{cases} | ||
| + | S_0=0\\ | ||
| + | S_1=1\\ | ||
| + | S_{n}=-l(S_{n-2})+r(S_{n-1}) | ||
| + | \end{cases}$$ | ||
| + | |||
| + | |||
| + | を用いるなら | ||
| + | |||
| + | |||
| + | :$$z^n=C_{n}+S_{n}z=-l(S_{n-1})+(S_{n})z\\$$ | ||
| + | :$$\begin{array}{l} | ||
| + | z^1=&0+z\\ | ||
| + | z^2=&-l+rz\\ | ||
| + | z^3=&-rl+(-l+r^2)z\\ | ||
| + | z^4=&-(-l+r^2)l+(-2rl+r^3)z\\ | ||
| + | z^5=&-(-2rl+r^3)l+(-3r^2l+l^2+r^4)z\\ | ||
&\quad\quad\quad\vdots\\ | &\quad\quad\quad\vdots\\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | |||
| + | |||
| + | ちなみに、数列 $$S_n$$ の一般項は次の通りであり、$$z$$ を生成元とする第1種[[ガラパゴ数列]]と同一である。 | ||
| + | |||
| + | |||
| + | :$$\displaystyle S_{n}=\frac{\displaystyle\left(r+\sqrt{r^2-4l}\right)^n-\left(r-\sqrt{r^2-4l}\right)^n}{\displaystyle2^n\sqrt{r^2-4l}}=\displaystyle\frac{z^n-\overline{z}^{~n}}{z-\overline{z}}=\sum_{k=0}^{n-1}\overline{z}^{~k}\cdot z^{n-k-1}=\sum_{k=0}^{\lfloor (n-1)/2\rfloor}\binom{n-k-1}{k}r^{n-2k-1}l^{k}$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===絶対値が1のケース=== | ||
| + | |||
| + | $$z=e^{i\theta}$$ である場合、$$l=z\cdotp\bar{z}=|z|^2=1,~r=z+\bar{z}=2\mathrm{Re}(z)=2\cos\theta$$ であることから | ||
| + | |||
| + | |||
| + | :$$\begin{array}{l} | ||
| + | \begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}\begin{pmatrix}1\\z\end{pmatrix}&=\begin{pmatrix}0&1\\-z\cdotp\bar{z}&z+\bar{z}\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix}\\ | ||
| + | &=\begin{pmatrix}0&1\\-1&2\cos\theta\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix} | ||
| + | \end{array}$$ | ||
| + | |||
| + | |||
| + | ここで得られる数列 | ||
| + | |||
| + | :$$\begin{cases} | ||
| + | S_0=0\\ | ||
| + | S_1=1\\ | ||
| + | S_{n}=-(S_{n-2})+(2\cos\theta)(S_{n-1}) | ||
| + | \end{cases}$$ | ||
| − | + | を用いるなら | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | :$$z^n=C_{n}+S_{n}z=-(S_{n-1})+(S_{n})z\\$$ | ||
:$$\begin{array}{l} | :$$\begin{array}{l} | ||
| − | z^1&=z&\\ | + | z^1&=0+z&\\ |
| − | z^2&= | + | z^2 |
| − | z^3&=(r^2 | + | &=-1+rz\\ |
| − | z^4&=(r^ | + | &=-1+(2\cos\theta)z\\ |
| − | z^5&=(r^ | + | z^3 |
| + | &=-r+(-1+r^2)z\\ | ||
| + | &=-(2\cos\theta)+[(2\cos\theta)^2-1]z\\ | ||
| + | &=-(2\cos\theta)+[2\cos2\theta+1]z\\ | ||
| + | z^4 | ||
| + | &=-(-1+r^2)+(-2r+r^3)z\\ | ||
| + | &=-[(2\cos\theta)^2-1]+[(2\cos\theta)^3-2(2\cos\theta)]z\\ | ||
| + | &=-[2\cos2\theta+1]+[2(\cos\theta+\cos3\theta)]z\\ | ||
| + | z^5 | ||
| + | &=-(-2r+r^3)+(-3r^2+1+r^4)z\\ | ||
| + | &=-[(2\cos\theta)^3-2(2\cos\theta)]+[(2\cos\theta)^4-3(2\cos\theta)^2+1]z\\ | ||
| + | &=-[2(\cos\theta+\cos3\theta)]+[2(\cos2\theta+\cos4\theta)+1]z\\ | ||
&\quad\quad\quad\vdots\\ | &\quad\quad\quad\vdots\\ | ||
| + | z^{2m} | ||
| + | &\displaystyle=-\left[1+2\sum_{k=1}^{m-1}\cos2k\theta\right]+\left[2\sum_{k=0}^{m-1}\cos(2k+1)\theta\right]z\\ | ||
| + | z^{2m+1} | ||
| + | &\displaystyle=-\left[2\sum_{k=0}^{m-1}\cos(2k+1)\theta\right]+\left[1+2\sum_{k=1}^{m}\cos2k\theta\right]z\\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | |||
| + | |||
| + | と表せる。この場合の数列 $$S_n$$ の一般項は次の通りであり、同じく $$z$$ を生成元とする第1種[[ガラパゴ数列]]と同一である。 | ||
| + | |||
| + | |||
| + | :$$\displaystyle S_{n}=\frac{\displaystyle\left(\cos\theta+i\sin\theta\right)^n-\left(\cos\theta-i\sin\theta\right)^n}{\displaystyle2i\sin\theta}\left(=\frac{\sin n\theta}{\sin\theta}\right)=\sum_{k=0}^{\lfloor (n-1)/2\rfloor}\binom{n-k-1}{k}(-1)^k(2\cos\theta)^{n-2k-1}$$ | ||
==導出== | ==導出== | ||
| 50行目: | 106行目: | ||
\begin{align*} | \begin{align*} | ||
z^2=&z\cdot z\\ | z^2=&z\cdot z\\ | ||
| − | =&( | + | =&(-\bar{z}+\bar{z}+z)z\\ |
| − | =&( | + | =&-(\bar{z}\cdotp z)+(\bar{z}+z)z\\ |
\end{align*} | \end{align*} | ||
| − | ここで、$$ | + | ここで、$$l=\bar{z}\cdotp z,~r=(\bar{z}+z)$$ と置くと |
\begin{align*} | \begin{align*} | ||
| − | z^2=rz | + | z^2=-l+rz |
\end{align*} | \end{align*} | ||
| − | 両辺に $$z$$ を乗じると $$z^3=rz^2 | + | 両辺に $$z$$ を乗じると $$z^3=-lz+rz^2$$ となり、右辺に $$z^2=-l+rz$$ を代入することで一次結合の形へと変形できる。この操作を再帰的に繰り返すことで、任意の整数乗を同形へと帰結させられる。※この導出手順は、分配則や結合則を満たし共役同士の和と積を求めることができる数(四元数など)であれば $$z\in\mathbb{C}$$ の範囲に限らず適用可能であることを示している。 |
| − | + | この $$z^2=-l+rz$$ は $$+1$$ と $$z$$ を基底の元とする斜交座標形式の複素数であり、$$z^2$$ の指し示す座標は $$(-l,r)$$、それぞれの元の指し示す座標は $$(1,0)$$ と $$(0,1)$$ である。ここで $$z$$ と $$z^2$$ を基底の元とする新たな斜交座標系を想定するとそれぞれの元が指し示す座標は旧座標系で $$(0,1)$$ と $$(-l,r)$$ であるため、基底は $$\begin{pmatrix}0&-l\\1&r\end{pmatrix}$$ と表される。旧座標系の基底と比べると原点を中心に $$\mathrm{Arg}~z~(\mathrm{rad})$$ 傾いた姿勢をとっているため、これを累乗することで任意の指数における基底の元の座標を得る。([[ガラパゴ数学]]の乗算の項を参照) | |
| − | == | + | |
| + | ==幾何イメージ== | ||
複素平面上の $$0$$ を始点とし $$+1$$ を終点とする位置ベクトル $$\vec{s}$$ と、同じく $$0$$ を始点とし任意の複素数 $$z$$ を終点とする位置ベクトル $$\vec{t}$$ において、原点を中心として $$\vec{s}$$ と $$\vec{t}$$ の成す角度の整数倍だけ $$\vec{t}$$ を回転させて得られる新たな位置ベクトル $$\vec{t'}$$ は、$$\vec{s}$$ と $$\vec{t}$$ を基底の元とするベクトル空間上の1次結合の形で表現可能である。 | 複素平面上の $$0$$ を始点とし $$+1$$ を終点とする位置ベクトル $$\vec{s}$$ と、同じく $$0$$ を始点とし任意の複素数 $$z$$ を終点とする位置ベクトル $$\vec{t}$$ において、原点を中心として $$\vec{s}$$ と $$\vec{t}$$ の成す角度の整数倍だけ $$\vec{t}$$ を回転させて得られる新たな位置ベクトル $$\vec{t'}$$ は、$$\vec{s}$$ と $$\vec{t}$$ を基底の元とするベクトル空間上の1次結合の形で表現可能である。 | ||
| 71行目: | 128行目: | ||
| − | |||
| − | |||
| − | === | + | ==実数の累乗と数列== |
| − | $$+1$$ | + | |
| + | $$z=\left(\frac{r}2\right)+\left(\mp\sqrt{l-\left(\frac{r}2\right)^2}\right)i$$ は $$z^2=-l+rz$$ の解 であり、 | ||
| + | |||
| + | :$$l=\bar{z}\cdot z$$ | ||
| + | :$$r=\bar{z}+z$$ | ||
| + | |||
| + | であるため、本定理より次の三項間漸化式による数列を得る。 | ||
| + | |||
| + | |||
| + | :$$\begin{cases} | ||
| + | S_0=0\\ | ||
| + | S_1=1\\ | ||
| + | S_{n}=-l(S_{n-2})+r(S_{n-1}) | ||
| + | \end{cases}$$ | ||
| + | |||
| + | |||
| + | ここで、$$l\leqq\left(\frac{r}2\right)^2$$ のとき $$z$$ は実数となるため実際の虚部は $$0$$ ということになる。 | ||
| + | |||
| + | |||
| + | しかし、$$z=a+b=(a)+\left(-\sqrt{-b^2}\right)i$$ と虚部を任意に解釈した場合にも | ||
| + | |||
| + | :$$l=\bar{z}\cdot z=a^2-b^2$$ | ||
| + | :$$r=\bar{z}+z=2a$$ | ||
| + | |||
| + | であり、$$z^2=-(a^2-b^2)+2az$$ は $$z=a+b$$ において真である。 | ||
| + | |||
| + | |||
| + | また、 | ||
| + | |||
| + | $$\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}=\begin{pmatrix}0&1\\-(a^2-b^2)&2a\end{pmatrix}^n$$ あるいは $$\begin{pmatrix}S_{n+1}\\S_{n}\end{pmatrix}=\begin{pmatrix}2a&-(a^2-b^2)\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix}$$ より得られる数列 | ||
| + | |||
| + | |||
| + | :$$\begin{cases} | ||
| + | S_0=0\\ | ||
| + | S_1=1\\ | ||
| + | S_{n}=-(a^2-b^2)(S_{n-2})+2a(S_{n-1}) | ||
| + | \end{cases}$$ | ||
| + | |||
| + | |||
| + | を用いても、一般項 $$S_{n}=\frac{\displaystyle(a+b)^n-(a-b)^n}{\displaystyle2b}$$ より | ||
| + | |||
| + | |||
| + | :$$\begin{array}{rl} | ||
| + | z^n=&C_{n}+S_{n}z\\ | ||
| + | =&-(a^2-b^2)(S_{n-1})+(a+b)(S_{n})\\ | ||
| + | =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)^n]-(a^2-b^2)[(a+b)^{n-1}-(a-b)^{n-1}]}{2b}\\ | ||
| + | =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)^n]-(a+b)[(a-b)(a+b)^{n-1}-(a-b)^n]}{2b}\\ | ||
| + | =&\displaystyle\frac{(a+b)[(a+b)^n]-(a+b)[(a-b)(a+b)^{n-1}]}{2b}\\ | ||
| + | =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)(a+b)^{n-1}]}{2b}\\ | ||
| + | =&\displaystyle\frac{(a+b)^n[(a+b)-(a-b)]}{2b}\\ | ||
| + | =&(a+b)^n | ||
| + | \end{array}$$ | ||
| + | |||
| + | |||
| + | と真であることを確認できる。 | ||
| + | |||
| + | |||
| + | このことは、複素共役の捉え方を拡張することで実数の累乗にも本定理を応用可能であることを示している。 | ||
| − | |||
| + | ===黄金数とフィボナッチ数列=== | ||
| − | |||
| − | + | 黄金数を $$\displaystyle z=\phi=\frac{1+\sqrt5}2=\frac12-\frac{\sqrt{-5}}{2}i$$ とみなして解釈するならば | |
| − | 黄金数を $$z=\phi | ||
| − | :$$ | + | :$$l=\left(\frac12+\frac{\sqrt{-5}}2i\right)\left(\frac12-\frac{\sqrt{-5}}2i\right)=\left(\frac14+\frac{-5}4\right)=-1$$ |
| − | + | :$$r=\left(\frac12+\frac{\sqrt{-5}}2i\right)+\left(\frac12-\frac{\sqrt{-5}}2i\right)=1$$ | |
| 94行目: | 204行目: | ||
| − | + | $$\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}=\begin{pmatrix}0&1\\1&1\end{pmatrix}^n$$ あるいは $$\begin{pmatrix}S_{n+1}\\S_{n}\end{pmatrix}=\begin{pmatrix}1&1\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix}$$ より得られる | |
| − | + | ||
| − | + | ||
| − | + | 数列 $$\begin{cases} | |
| − | \end{ | + | S_0=0\\ |
| + | S_1=1\\ | ||
| + | S_{n}=(S_{n-2})+(S_{n-1}) | ||
| + | \end{cases}$$ または | ||
| + | |||
| + | |||
| + | 一般項 $$S_{n}=\frac{\displaystyle\left(1+\sqrt{5}\right)^n-\left(1-\sqrt{5}\right)^n}{\displaystyle2^n\sqrt{5}}$$ | ||
| + | |||
| + | |||
| + | を用いて | ||
| + | |||
| + | |||
| + | :$$z^n=C_{n}+S_{n}z=(S_{n-1})+(S_{n})z\\$$ | ||
| + | |||
| + | |||
| + | が導かれる。この $$S_n$$ と $$z^n$$ は黄金数とフィボナッチ数列の関係式 | ||
| + | |||
| + | |||
| + | :$$\displaystyle F_n=\frac{\phi^n-(-\phi)^{-n}}{\sqrt{5}}$$ | ||
| + | :$$\phi^n=F_{n-1}+F_n\phi$$ | ||
| + | |||
| + | と同一であることが分かる。 | ||
| − | |||
| − | + | ==応用== | |
| + | ===ガラパゴ三辺比定理=== | ||
| + | ユークリッド平面上の三角形 $$\triangle OAB$$ において、長さが $$x$$ の辺 $$OA$$ と 長さが $$y$$ の辺 $$AB$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、辺 $$OB$$ を $$O$$ を中心として $$\angle O$$ の偶数倍回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表せるという定理である。本定理を用いることで容易に導出できるが、詳しくは[[ガラパゴ三辺比定理]]を参照のこと。 | ||
| − | + | ===ガラパゴ三角関数=== | |
| + | $$+1$$ と $$z=e^{i\theta}$$ を理論上の基底の元($$z$$ が実数であっても独立した元であるものとみなして区別)とする斜交座標系において、極座標 $$e^{xz}$$ の示す座標を基底の元の線形結合で表現したときの各元の係数を得る関数として次のような等式を想定する。 | ||
| − | :$$ | + | :$$e^{xz}=\cos_zx+z\sin_zx$$ |
| − | + | これらの関数 $$\cos_zx$$ と $$\sin_zx$$ は、本定理と非常に密接な関係にある。詳しくは[[ガラパゴ三角関数]]を参照のこと。 | |
2025年3月10日 (月) 15:23時点における最新版
ガラパゴ累乗定理(ガラパゴるいじょうていり)とは、複素数 $$z$$ の累乗は $$z+\overline{z}$$ と $$z\cdot\overline{z}$$ を元とする多項式より生成される実数を係数とする $$z$$ の一次式で表せるという定理である。
ガラパゴ数学の主定理の一つで、$$+1$$ と $$+z$$ を基底の元とする $$\mathbb{R}^2$$ 斜交平面上の幾何を扱うことを主目的として みゆ によって導出された。
概要
複素数 $$z$$ の 整数 $$n$$ 乗は、$$l=z\cdotp\bar{z}=|z|^2$$ と $$r=z+\bar{z}=2\mathrm{Re}(z)$$ を用いて次のように表せる。
- $$\begin{array}{l} \begin{pmatrix} z^n\\z^{n+1}\end{pmatrix}&=\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}\begin{pmatrix}1\\z\end{pmatrix}\\ &=\begin{pmatrix}0&1\\-l&r\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix}=\begin{pmatrix}0&1\\-z\cdotp\bar{z}&z+\bar{z}\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix} \end{array}$$
ここで得られる数列
- $$\begin{cases} S_0=0\\ S_1=1\\ S_{n}=-l(S_{n-2})+r(S_{n-1}) \end{cases}$$
を用いるなら
- $$z^n=C_{n}+S_{n}z=-l(S_{n-1})+(S_{n})z\\$$
- $$\begin{array}{l} z^1=&0+z\\ z^2=&-l+rz\\ z^3=&-rl+(-l+r^2)z\\ z^4=&-(-l+r^2)l+(-2rl+r^3)z\\ z^5=&-(-2rl+r^3)l+(-3r^2l+l^2+r^4)z\\ &\quad\quad\quad\vdots\\ \end{array}$$
ちなみに、数列 $$S_n$$ の一般項は次の通りであり、$$z$$ を生成元とする第1種ガラパゴ数列と同一である。
- $$\displaystyle S_{n}=\frac{\displaystyle\left(r+\sqrt{r^2-4l}\right)^n-\left(r-\sqrt{r^2-4l}\right)^n}{\displaystyle2^n\sqrt{r^2-4l}}=\displaystyle\frac{z^n-\overline{z}^{~n}}{z-\overline{z}}=\sum_{k=0}^{n-1}\overline{z}^{~k}\cdot z^{n-k-1}=\sum_{k=0}^{\lfloor (n-1)/2\rfloor}\binom{n-k-1}{k}r^{n-2k-1}l^{k}$$
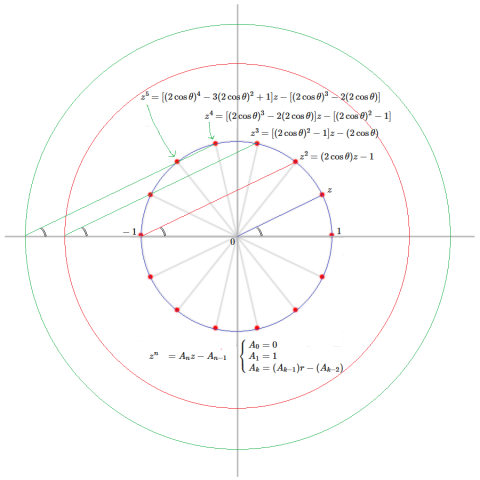
絶対値が1のケース
$$z=e^{i\theta}$$ である場合、$$l=z\cdotp\bar{z}=|z|^2=1,~r=z+\bar{z}=2\mathrm{Re}(z)=2\cos\theta$$ であることから
- $$\begin{array}{l} \begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}\begin{pmatrix}1\\z\end{pmatrix}&=\begin{pmatrix}0&1\\-z\cdotp\bar{z}&z+\bar{z}\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix}\\ &=\begin{pmatrix}0&1\\-1&2\cos\theta\end{pmatrix}^n\begin{pmatrix}1\\z\end{pmatrix} \end{array}$$
ここで得られる数列
- $$\begin{cases} S_0=0\\ S_1=1\\ S_{n}=-(S_{n-2})+(2\cos\theta)(S_{n-1}) \end{cases}$$
を用いるなら
- $$z^n=C_{n}+S_{n}z=-(S_{n-1})+(S_{n})z\\$$
- $$\begin{array}{l} z^1&=0+z&\\ z^2 &=-1+rz\\ &=-1+(2\cos\theta)z\\ z^3 &=-r+(-1+r^2)z\\ &=-(2\cos\theta)+[(2\cos\theta)^2-1]z\\ &=-(2\cos\theta)+[2\cos2\theta+1]z\\ z^4 &=-(-1+r^2)+(-2r+r^3)z\\ &=-[(2\cos\theta)^2-1]+[(2\cos\theta)^3-2(2\cos\theta)]z\\ &=-[2\cos2\theta+1]+[2(\cos\theta+\cos3\theta)]z\\ z^5 &=-(-2r+r^3)+(-3r^2+1+r^4)z\\ &=-[(2\cos\theta)^3-2(2\cos\theta)]+[(2\cos\theta)^4-3(2\cos\theta)^2+1]z\\ &=-[2(\cos\theta+\cos3\theta)]+[2(\cos2\theta+\cos4\theta)+1]z\\ &\quad\quad\quad\vdots\\ z^{2m} &\displaystyle=-\left[1+2\sum_{k=1}^{m-1}\cos2k\theta\right]+\left[2\sum_{k=0}^{m-1}\cos(2k+1)\theta\right]z\\ z^{2m+1} &\displaystyle=-\left[2\sum_{k=0}^{m-1}\cos(2k+1)\theta\right]+\left[1+2\sum_{k=1}^{m}\cos2k\theta\right]z\\ \end{array}$$
と表せる。この場合の数列 $$S_n$$ の一般項は次の通りであり、同じく $$z$$ を生成元とする第1種ガラパゴ数列と同一である。
- $$\displaystyle S_{n}=\frac{\displaystyle\left(\cos\theta+i\sin\theta\right)^n-\left(\cos\theta-i\sin\theta\right)^n}{\displaystyle2i\sin\theta}\left(=\frac{\sin n\theta}{\sin\theta}\right)=\sum_{k=0}^{\lfloor (n-1)/2\rfloor}\binom{n-k-1}{k}(-1)^k(2\cos\theta)^{n-2k-1}$$
導出
$$\{z\in\mathbb{C}\}$$ において、$$\mathbb{R}^2$$ 上の複素数 $$z$$ を次のように二乗する。
\begin{align*} z^2=&z\cdot z\\ =&(-\bar{z}+\bar{z}+z)z\\ =&-(\bar{z}\cdotp z)+(\bar{z}+z)z\\ \end{align*}
ここで、$$l=\bar{z}\cdotp z,~r=(\bar{z}+z)$$ と置くと
\begin{align*} z^2=-l+rz \end{align*}
両辺に $$z$$ を乗じると $$z^3=-lz+rz^2$$ となり、右辺に $$z^2=-l+rz$$ を代入することで一次結合の形へと変形できる。この操作を再帰的に繰り返すことで、任意の整数乗を同形へと帰結させられる。※この導出手順は、分配則や結合則を満たし共役同士の和と積を求めることができる数(四元数など)であれば $$z\in\mathbb{C}$$ の範囲に限らず適用可能であることを示している。
この $$z^2=-l+rz$$ は $$+1$$ と $$z$$ を基底の元とする斜交座標形式の複素数であり、$$z^2$$ の指し示す座標は $$(-l,r)$$、それぞれの元の指し示す座標は $$(1,0)$$ と $$(0,1)$$ である。ここで $$z$$ と $$z^2$$ を基底の元とする新たな斜交座標系を想定するとそれぞれの元が指し示す座標は旧座標系で $$(0,1)$$ と $$(-l,r)$$ であるため、基底は $$\begin{pmatrix}0&-l\\1&r\end{pmatrix}$$ と表される。旧座標系の基底と比べると原点を中心に $$\mathrm{Arg}~z~(\mathrm{rad})$$ 傾いた姿勢をとっているため、これを累乗することで任意の指数における基底の元の座標を得る。(ガラパゴ数学の乗算の項を参照)
幾何イメージ
複素平面上の $$0$$ を始点とし $$+1$$ を終点とする位置ベクトル $$\vec{s}$$ と、同じく $$0$$ を始点とし任意の複素数 $$z$$ を終点とする位置ベクトル $$\vec{t}$$ において、原点を中心として $$\vec{s}$$ と $$\vec{t}$$ の成す角度の整数倍だけ $$\vec{t}$$ を回転させて得られる新たな位置ベクトル $$\vec{t'}$$ は、$$\vec{s}$$ と $$\vec{t}$$ を基底の元とするベクトル空間上の1次結合の形で表現可能である。
実数の累乗と数列
$$z=\left(\frac{r}2\right)+\left(\mp\sqrt{l-\left(\frac{r}2\right)^2}\right)i$$ は $$z^2=-l+rz$$ の解 であり、
- $$l=\bar{z}\cdot z$$
- $$r=\bar{z}+z$$
であるため、本定理より次の三項間漸化式による数列を得る。
- $$\begin{cases} S_0=0\\ S_1=1\\ S_{n}=-l(S_{n-2})+r(S_{n-1}) \end{cases}$$
ここで、$$l\leqq\left(\frac{r}2\right)^2$$ のとき $$z$$ は実数となるため実際の虚部は $$0$$ ということになる。
しかし、$$z=a+b=(a)+\left(-\sqrt{-b^2}\right)i$$ と虚部を任意に解釈した場合にも
- $$l=\bar{z}\cdot z=a^2-b^2$$
- $$r=\bar{z}+z=2a$$
であり、$$z^2=-(a^2-b^2)+2az$$ は $$z=a+b$$ において真である。
また、
$$\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}=\begin{pmatrix}0&1\\-(a^2-b^2)&2a\end{pmatrix}^n$$ あるいは $$\begin{pmatrix}S_{n+1}\\S_{n}\end{pmatrix}=\begin{pmatrix}2a&-(a^2-b^2)\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix}$$ より得られる数列
- $$\begin{cases} S_0=0\\ S_1=1\\ S_{n}=-(a^2-b^2)(S_{n-2})+2a(S_{n-1}) \end{cases}$$
を用いても、一般項 $$S_{n}=\frac{\displaystyle(a+b)^n-(a-b)^n}{\displaystyle2b}$$ より
- $$\begin{array}{rl} z^n=&C_{n}+S_{n}z\\ =&-(a^2-b^2)(S_{n-1})+(a+b)(S_{n})\\ =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)^n]-(a^2-b^2)[(a+b)^{n-1}-(a-b)^{n-1}]}{2b}\\ =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)^n]-(a+b)[(a-b)(a+b)^{n-1}-(a-b)^n]}{2b}\\ =&\displaystyle\frac{(a+b)[(a+b)^n]-(a+b)[(a-b)(a+b)^{n-1}]}{2b}\\ =&\displaystyle\frac{(a+b)[(a+b)^n-(a-b)(a+b)^{n-1}]}{2b}\\ =&\displaystyle\frac{(a+b)^n[(a+b)-(a-b)]}{2b}\\ =&(a+b)^n \end{array}$$
と真であることを確認できる。
このことは、複素共役の捉え方を拡張することで実数の累乗にも本定理を応用可能であることを示している。
黄金数とフィボナッチ数列
黄金数を $$\displaystyle z=\phi=\frac{1+\sqrt5}2=\frac12-\frac{\sqrt{-5}}{2}i$$ とみなして解釈するならば
- $$l=\left(\frac12+\frac{\sqrt{-5}}2i\right)\left(\frac12-\frac{\sqrt{-5}}2i\right)=\left(\frac14+\frac{-5}4\right)=-1$$
- $$r=\left(\frac12+\frac{\sqrt{-5}}2i\right)+\left(\frac12-\frac{\sqrt{-5}}2i\right)=1$$
であるため、
$$\begin{pmatrix}C_{n}&S_{n}\\C_{n+1}&S_{n+1}\end{pmatrix}=\begin{pmatrix}0&1\\1&1\end{pmatrix}^n$$ あるいは $$\begin{pmatrix}S_{n+1}\\S_{n}\end{pmatrix}=\begin{pmatrix}1&1\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix}$$ より得られる
数列 $$\begin{cases}
S_0=0\\
S_1=1\\
S_{n}=(S_{n-2})+(S_{n-1})
\end{cases}$$ または
一般項 $$S_{n}=\frac{\displaystyle\left(1+\sqrt{5}\right)^n-\left(1-\sqrt{5}\right)^n}{\displaystyle2^n\sqrt{5}}$$
を用いて
- $$z^n=C_{n}+S_{n}z=(S_{n-1})+(S_{n})z\\$$
が導かれる。この $$S_n$$ と $$z^n$$ は黄金数とフィボナッチ数列の関係式
- $$\displaystyle F_n=\frac{\phi^n-(-\phi)^{-n}}{\sqrt{5}}$$
- $$\phi^n=F_{n-1}+F_n\phi$$
と同一であることが分かる。
応用
ガラパゴ三辺比定理
ユークリッド平面上の三角形 $$\triangle OAB$$ において、長さが $$x$$ の辺 $$OA$$ と 長さが $$y$$ の辺 $$AB$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、辺 $$OB$$ を $$O$$ を中心として $$\angle O$$ の偶数倍回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表せるという定理である。本定理を用いることで容易に導出できるが、詳しくはガラパゴ三辺比定理を参照のこと。
ガラパゴ三角関数
$$+1$$ と $$z=e^{i\theta}$$ を理論上の基底の元($$z$$ が実数であっても独立した元であるものとみなして区別)とする斜交座標系において、極座標 $$e^{xz}$$ の示す座標を基底の元の線形結合で表現したときの各元の係数を得る関数として次のような等式を想定する。
- $$e^{xz}=\cos_zx+z\sin_zx$$
これらの関数 $$\cos_zx$$ と $$\sin_zx$$ は、本定理と非常に密接な関係にある。詳しくはガラパゴ三角関数を参照のこと。