数列と微分積分

この記事は主に高校数学においての数列と微分積分法の分野の関係についての独自研究である。 なお、この記事は編集中である。

はじめに

高校数学では数列と関数は全くの別物のように扱われているが、数列も主に自然数に対して定義されている歴とした関数である。

極限を扱う微分積分よりも以下に述べる和分差分は直感的に分かりやすい為、数列だけでなく微分積分の見方も変わるかも知れない。

微分法と差分法

関数 $$f(x)$$ に対して

$$\displaystyle{\frac d{dx}f(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}h}$$

なる $$\frac d{dx}f(x)$$ が $$f(x)$$ の微分であった。

ここで $$h\to0$$ という極限を取るのではなく $$h=1$$ と固定すると

$$\displaystyle{\Delta f(x)=f(x+1)-f(x)}$$

となる。 このとき$$\Delta f(x)$$を$$f(x)$$の差分と呼ぶ。 これは階差数列でもある。

また、微分と同様に $$f(x)$$ の定数項は $$\Delta f(x)$$ に関係がないことは微分よりも明確にわかる。

積分法と和分法

定積分と定和分

$$\displaystyle{\sum\nolimits_a^bf(x)=\sum_{x=a}^{b-1}f(x)}$$

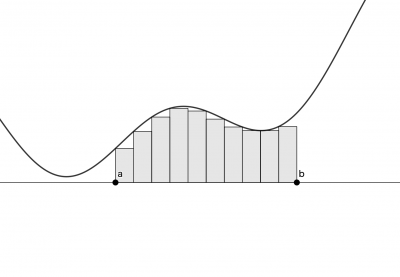
で表される $$\sum\nolimits_a^bf(x)$$ を $$f(x)$$ の $$a$$ から $$b$$ までの定和分と呼び、上図の灰色の部分の面積を表す。 なお、終点 $$b$$ は含まれないことに注意する。

この時上図の長方形の横幅はそれぞれ $$1$$ であるが、この幅の $$0$$ への極限をとった時の面積が

$$\displaystyle{\int_a^bf(x)\,dx}$$

であり、 $$f(x)$$ の $$a$$ から $$b$$ までの定積分である。

不定積分と不定和分

微分の逆演算をしたもの、すなわち

$$\displaystyle{\frac d{dx}\int f(x)\,dx=f(x)}$$

を満たす $$\int f(x)\,dx$$ を $$f(x)$$ の不定積分と呼んだが、差分の逆演算をしたもの、すなわち

$$\displaystyle{\Delta \sum f(x)=f(x)}$$

を満たす $$\sum f(x)$$ を $$f(x)$$ の不定和分と呼ぶ。

上述の通り差分は元の関数の定数項に関係ないため、不定和分は不定積分と同様に和分定数が生じる。

和分差分学の基本定理

$$\displaystyle{\begin{align*} \Delta\sum\nolimits_a^xf(t) &=\Delta\sum_{n=a}^{x-1}f(n)\\ &=\sum_{n=a}^{x}f(n)-\sum_{n=a}^{x-1}f(n)\\ &=\{f(x)+f(x-1)+\cdots+f(a)\}-\{f(x-1)+f(x-2)+\cdots+f(a)\}\\ &=f(x) \end{align*}}$$

よって

$$\displaystyle{\Delta\sum\nolimits_a^xf(t)=f(x)}$$

となる。

また、$$F(x)=\sum f(x)$$ とした時

$$\displaystyle{\sum\nolimits_a^bf(t)=F(b)-F(a)}$$

が成立する。前節のグラフを見ても分かるし、1項ずつ書き出しても分かるだろう。

これは微分積分学の基本定理に対応する。

和分差分の性質

線形性

$$\displaystyle{\Delta kf(x)=k\Delta f(x)}$$

$$\displaystyle{\Delta\{f(x)+g(x)\}=\Delta f(x)+\Delta g(x)}$$

$$\displaystyle{\sum kf(x)=k\sum f(x)}$$

$$\displaystyle{\sum \{f(x)+g(x)\}=\sum f(x)+\sum g(x)}$$

下降階乗

正の整数 $$n$$ に対して下降階乗 $$x^{\underline n}$$ を

$$x^{\underline n}=x(x-1)(x-2)\cdots(x-n+1)$$

と定義する。

差分をとると

$$\begin{align*} \Delta x^{\underline n} &=(x+1)x(x-1)(x-2)\cdots(x-n+2)-x(x-1)(x-2)\cdots(x-n+1)\\ &=\{(x+1)-(x-n+1)\}x(x-1)(x-2)\cdots(x-n+2)\\ &=nx^{\underline{n-1}} \end{align*}$$

となり、和分差分学の基本定理より

$$\displaystyle{\sum x^{\underline n}=\frac{x^{\underline{n+1}}}{n+1}}+\text{const.}$$

が従う。 これは $$x^n$$ の微分積分に対応する。

またこの性質を用いると、

$$\displaystyle{\begin{align*} \sum_{x=1}^nx^2 &=\sum\nolimits_1^{n+1}x^2\\ &=\sum\nolimits_1^{n+1}\{x(x-1)+x\}\\ &=\sum\nolimits_1^{n+1}\{x^{\underline2}+x^{\underline1}\}\\ &=\left[\frac{x^{\underline3}}3+\frac{x^{\underline2}}2\right]_1^{n+1}\\ &=\frac16n(n+1)(2n+1) \end{align*}}$$

など $$n$$ 乗の和の公式を導くことができる。

積の差分と部分和分

積の微分に対して積の差分は

$$\displaystyle{\begin{align*} \Delta\{f(x)g(x)\} &=f(x+1)g(x+1)-f(x)g(x)\\ &=f(x)g(x+1)-f(x)g(x)+f(x+1)g(x+1)-f(x)g(x+1)\\ &=f(x)\Delta g(x)+g(x+1)\Delta f(x) \end{align*}}$$

となり、両辺を和分し整理することによって部分和分

$$\displaystyle{\sum f(x)\Delta g(x)=f(x)g(x)-\sum g(x+1)\Delta f(x)}$$

$$\displaystyle{\sum\nolimits_a^b f(x)\Delta g(x)=\left[f(x)g(x)\right]_a^b-\sum\nolimits_a^b g(x+1)\Delta f(x)}$$

を導ける。