「ガラパゴ三辺比定理」の版間の差分
| 1行目: | 1行目: | ||
| − | '''みゆの三辺比定理'''(みゆのさんぺんひていり)とは、ユークリッド平面上の三角形 $$\triangle ABC$$ | + | '''みゆの三辺比定理'''(みゆのさんぺんひていり)とは、ユークリッド平面上の三角形 $$\triangle ABC$$ において、長さが $$x$$ の辺 $$AB$$ と 長さが $$y$$ の辺 $$AC$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、$$\angle B$$ の角度を偶数倍すなわち辺 $$BC$$ を $$B$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$c=\cos\theta$$ の整式で表せるという定理である。[[ガラパゴ数学]]の主定理の一つで、特に $$\theta=\frac{\pi}{2}~\mathrm{rad}$$ の場合は'''ピタゴラスの定理II'''、'''ピタツー'''などの愛称で呼ばれることもある。 |
==概要== | ==概要== | ||
| − | 辺 $$AB$$ の長さが $$x$$、辺 $$AC$$ の長さが $$y$$、これら二辺の成す内角が $$\theta~\mathrm{rad}$$ であるようなユークリッド平面上の三角形 $$\triangle ABC$$ | + | 辺 $$AB$$ の長さが $$x$$、辺 $$AC$$ の長さが $$y$$、これら二辺の成す内角が $$\theta~\mathrm{rad}$$ であるようなユークリッド平面上の三角形 $$\triangle ABC$$ の三辺比は次の通りである。 |
| + | :$$x$$ : $$y$$ : $$\sqrt{x^2+y^2-2xy\cos\theta}$$ | ||
| + | この三辺比は、$$AB$$ 上に $$\angle BA'C$$ が直角となるような点 $$A'$$ を置くことで(その直角を挟む辺の長さが $$x+y\cos(\pi-\theta)$$ と $$y\sin(\pi-\theta)$$ であることから)容易に導出できるが、三平方の定理に起因する平方根項が存在するため整式の比とはなっていない。 | ||
| + | |||
| + | しかし、$$\angle B$$ を偶数倍すなわち辺 $$BC$$ を $$B$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$c=\cos\theta$$ の整式で表すことができる。 | ||
| + | |||
| + | $$\angle B$$ を2倍した場合 | ||
| − | :$$x^2-y^2$$ : $$2xy- | + | :$$x^2-y^2$$ : $$2xy-2cy^2$$ : $$x^2+y^2-2cxy$$ |
| − | + | $$\angle B$$ を4倍した場合 | |
| + | :$$x^4+y^4-6x^2y^2+8cxy^3-4c^2y^4$$ : $$-4x^3y+4xy^3+12cx^2y^2-4cy^4-16c^2xy^3+8c^3y^4$$ : $$(x^2+y^2-2cxy)^2$$ | ||
| − | |||
| − | + | このとき、三辺比の第一項と第二項に対応する二辺の成す角の角度が $$\theta~\mathrm{rad}$$ となる。ここでいう二辺の成す角とは必ずしも内角を指すものではない。辺 $$AB$$ と辺 $$AC$$ の伸縮によっていずれか一方のみが負数倍となる場合は内角と外角が入れ替わるため、その場合は外角が $$\theta~\mathrm{rad}$$ であり、内角としては $$\pi-\theta~\mathrm{rad}$$ となる。 | |
| − | + | 角度を偶数倍することの意味は、平方根項に対応する辺 $$BC$$ の長さを $$1$$ とする相似比 $$1$$ : $$BC$$ の相似三角形を作る([[ガラパゴ数学]]の乗算の項を参照)ことで $$BC$$ に対応する辺の長さの2乗を作り出すことにある。従って、角度を偶数倍すれば偶数乗により根号は外れる。 | |
==導出== | ==導出== | ||
| 23行目: | 29行目: | ||
角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、 | 角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、 | ||
:$$x$$ : $$y$$ : $$|x+yz|$$ | :$$x$$ : $$y$$ : $$|x+yz|$$ | ||
| − | + | である。この三角形の第三項 $$|x+yz|$$ に対応する辺を 第一項 $$x$$ に対応する辺との交点を中心にそれらの狭角が2倍になるように回転した線分を延長して得られる直線は、$$x+yz$$ を $$+1$$ とみなした相似な座標系においても $$x+yz$$ を通るため | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:$$(x+yz)\times(x+yz)=x^2+y^2z^2+2xyz$$ | :$$(x+yz)\times(x+yz)=x^2+y^2z^2+2xyz$$ | ||
| − | + | を通るといえる。([[ガラパゴ数学]]の乗算の項を参照) | |
この座標は[[みゆの累乗定理]]によって | この座標は[[みゆの累乗定理]]によって | ||
| 39行目: | 39行目: | ||
=&(x^2-y^2)+(2xy-2y^2\cos\theta)z\\ | =&(x^2-y^2)+(2xy-2y^2\cos\theta)z\\ | ||
\end{align} | \end{align} | ||
| − | と $$z$$ | + | と $$z$$ の一次式の形で表すことができる。 |
| + | |||
| + | これによって示された新たな三角形の三辺比は | ||
:$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$ | :$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$ | ||
| − | + | であるが、$$z=e^{i(\pi-\theta)}=\cos(\pi-\theta)+i\sin(\pi-\theta)$$ であるため | |
| + | \begin{align} | ||
| + | |x+yz|=&\big|[x+y\cos(\pi-\theta)]+[y\sin(\pi-\theta)]i\big|\\ | ||
| + | =&\sqrt{[x+y\cos(\pi-\theta)]^2+[y\sin(\pi-\theta)]^2}\\ | ||
| + | =&\sqrt{(x-y\cos\theta)^2+(y\sin\theta)^2}\\ | ||
| + | =&\sqrt{x^2+y^2(\cos^2\theta+\sin^2\theta)-2xy\cos\theta}\\ | ||
| + | =&\sqrt{x^2+y^2-2xy\cos\theta} | ||
| + | \end{align} | ||
| + | によって | ||
:$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$ | :$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$ | ||
| − | + | と書き改めることができる。この比率は二辺の成す角が $$\theta~\mathrm{rad}$$ である三角形の三辺比といえる。 | |
| 49行目: | 59行目: | ||
| − | + | もし初めの操作で狭角が偶数倍になるように回転させた場合でも、偶数乘の相似比を想定することになるため $$|x+yz|$$ が偶数乗されて根号は外れる。 | |
==みゆの三辺比恒等式== | ==みゆの三辺比恒等式== | ||
| − | + | みゆの三辺比定理で示される三角形の三辺比より、以下の恒等式を導くことができる。 | |
| − | + | \begin{align} | |
| − | + | &(x^2+y^2-2xy\cos\theta)^2\\ | |
| + | =&\big[(x^2-y^2)+(2xy-2y^2\cos\theta)e^{\pi-\theta}\big|^2\\ | ||
| + | =&(x^2-y^2)^2+(2xy-2y^2\cos\theta)^2-2(x^2-y^2)(2xy-2y^2\cos\theta)\cos\theta | ||
| + | \end{align} | ||
==拡張ピタゴラス数== | ==拡張ピタゴラス数== | ||
2019年9月3日 (火) 12:11時点における版
みゆの三辺比定理(みゆのさんぺんひていり)とは、ユークリッド平面上の三角形 $$\triangle ABC$$ において、長さが $$x$$ の辺 $$AB$$ と 長さが $$y$$ の辺 $$AC$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、$$\angle B$$ の角度を偶数倍すなわち辺 $$BC$$ を $$B$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$c=\cos\theta$$ の整式で表せるという定理である。ガラパゴ数学の主定理の一つで、特に $$\theta=\frac{\pi}{2}~\mathrm{rad}$$ の場合はピタゴラスの定理II、ピタツーなどの愛称で呼ばれることもある。
概要
辺 $$AB$$ の長さが $$x$$、辺 $$AC$$ の長さが $$y$$、これら二辺の成す内角が $$\theta~\mathrm{rad}$$ であるようなユークリッド平面上の三角形 $$\triangle ABC$$ の三辺比は次の通りである。
- $$x$$ : $$y$$ : $$\sqrt{x^2+y^2-2xy\cos\theta}$$
この三辺比は、$$AB$$ 上に $$\angle BA'C$$ が直角となるような点 $$A'$$ を置くことで(その直角を挟む辺の長さが $$x+y\cos(\pi-\theta)$$ と $$y\sin(\pi-\theta)$$ であることから)容易に導出できるが、三平方の定理に起因する平方根項が存在するため整式の比とはなっていない。
しかし、$$\angle B$$ を偶数倍すなわち辺 $$BC$$ を $$B$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$c=\cos\theta$$ の整式で表すことができる。
$$\angle B$$ を2倍した場合
- $$x^2-y^2$$ : $$2xy-2cy^2$$ : $$x^2+y^2-2cxy$$
$$\angle B$$ を4倍した場合
- $$x^4+y^4-6x^2y^2+8cxy^3-4c^2y^4$$ : $$-4x^3y+4xy^3+12cx^2y^2-4cy^4-16c^2xy^3+8c^3y^4$$ : $$(x^2+y^2-2cxy)^2$$
このとき、三辺比の第一項と第二項に対応する二辺の成す角の角度が $$\theta~\mathrm{rad}$$ となる。ここでいう二辺の成す角とは必ずしも内角を指すものではない。辺 $$AB$$ と辺 $$AC$$ の伸縮によっていずれか一方のみが負数倍となる場合は内角と外角が入れ替わるため、その場合は外角が $$\theta~\mathrm{rad}$$ であり、内角としては $$\pi-\theta~\mathrm{rad}$$ となる。
角度を偶数倍することの意味は、平方根項に対応する辺 $$BC$$ の長さを $$1$$ とする相似比 $$1$$ : $$BC$$ の相似三角形を作る(ガラパゴ数学の乗算の項を参照)ことで $$BC$$ に対応する辺の長さの2乗を作り出すことにある。従って、角度を偶数倍すれば偶数乗により根号は外れる。
導出
$$+1$$ と $$z=e^{i(\pi-\theta)}$$ を元とする基底空間において、内角の一つに $$\theta~\mathrm{rad}$$ をもつ三角形を想定する。
角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、
- $$x$$ : $$y$$ : $$|x+yz|$$
である。この三角形の第三項 $$|x+yz|$$ に対応する辺を 第一項 $$x$$ に対応する辺との交点を中心にそれらの狭角が2倍になるように回転した線分を延長して得られる直線は、$$x+yz$$ を $$+1$$ とみなした相似な座標系においても $$x+yz$$ を通るため
- $$(x+yz)\times(x+yz)=x^2+y^2z^2+2xyz$$
を通るといえる。(ガラパゴ数学の乗算の項を参照)
この座標はみゆの累乗定理によって \begin{align} (x+yz)^2=&x^2+y^2(2z\cos(\pi-\theta)-1)+2xyz\\ =&x^2+y^2(-2z\cos\theta-1)+2xyz\\ =&(x^2-y^2)+(2xy-2y^2\cos\theta)z\\ \end{align} と $$z$$ の一次式の形で表すことができる。
これによって示された新たな三角形の三辺比は
- $$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$
であるが、$$z=e^{i(\pi-\theta)}=\cos(\pi-\theta)+i\sin(\pi-\theta)$$ であるため \begin{align} |x+yz|=&\big|[x+y\cos(\pi-\theta)]+[y\sin(\pi-\theta)]i\big|\\ =&\sqrt{[x+y\cos(\pi-\theta)]^2+[y\sin(\pi-\theta)]^2}\\ =&\sqrt{(x-y\cos\theta)^2+(y\sin\theta)^2}\\ =&\sqrt{x^2+y^2(\cos^2\theta+\sin^2\theta)-2xy\cos\theta}\\ =&\sqrt{x^2+y^2-2xy\cos\theta} \end{align} によって
- $$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$
と書き改めることができる。この比率は二辺の成す角が $$\theta~\mathrm{rad}$$ である三角形の三辺比といえる。
もし初めの操作で狭角が偶数倍になるように回転させた場合でも、偶数乘の相似比を想定することになるため $$|x+yz|$$ が偶数乗されて根号は外れる。
みゆの三辺比恒等式
みゆの三辺比定理で示される三角形の三辺比より、以下の恒等式を導くことができる。 \begin{align} &(x^2+y^2-2xy\cos\theta)^2\\ =&\big[(x^2-y^2)+(2xy-2y^2\cos\theta)e^{\pi-\theta}\big|^2\\ =&(x^2-y^2)^2+(2xy-2y^2\cos\theta)^2-2(x^2-y^2)(2xy-2y^2\cos\theta)\cos\theta \end{align}
拡張ピタゴラス数
二辺の成す角 $$θ$$ において $$\cos\theta$$ が有理数値であるような三角形の三辺比は、みゆの三辺比定理を用いると整数比で表すことができる。
ただし辺の長さが負の値をとる場合、内角と外角が入れ替わることに注意が必要である。その場合の内角は $$\pi-\theta~\mathrm{rad}$$ となる。
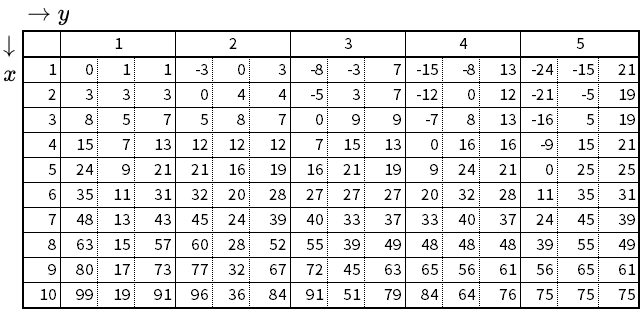
二辺の成す角が $$\theta=~\frac{\pi}{3}~\mathrm{rad}~(60^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy-y^2$$ : $$x^2+y^2-xy$$
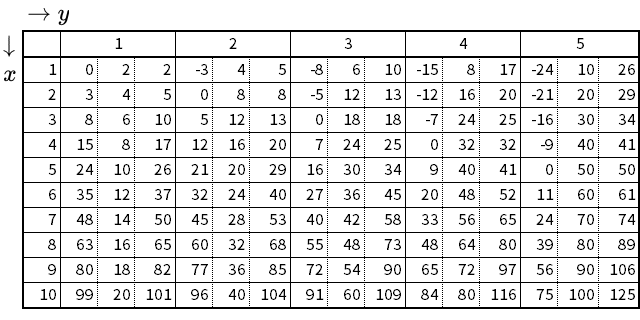
二辺の成す角が $$\theta=~\frac{\pi}{2}~\mathrm{rad}~(90^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy$$ : $$x^2+y^2$$
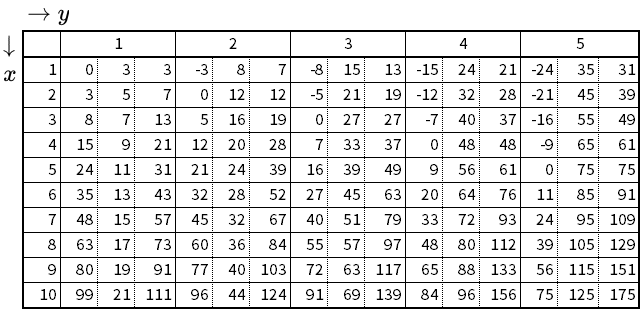
二辺の成す角が $$\theta=~\frac{2\pi}{3}~\mathrm{rad}~(120^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy+y^2$$ : $$x^2+y^2+xy$$