「数列と微分積分」の版間の差分
(→はじめに) |
|||
| (同じ利用者による、間の25版が非表示) | |||
| 5行目: | 5行目: | ||
==はじめに== | ==はじめに== | ||
高校数学では数列と関数は全くの別物のように扱われているが、数列も主に自然数に対して定義されている歴とした関数である。 | 高校数学では数列と関数は全くの別物のように扱われているが、数列も主に自然数に対して定義されている歴とした関数である。 | ||
| + | |||
| + | そのためここでは微分積分学との関係がわかりやすくなるよう数列を $$a_n$$ といった表記ではなく $$f(x)$$ という表記にする。 | ||
極限を扱う微分積分よりも以下に述べる和分差分は直感的に分かりやすい為、数列だけでなく微分積分の見方も変わるかも知れない。 | 極限を扱う微分積分よりも以下に述べる和分差分は直感的に分かりやすい為、数列だけでなく微分積分の見方も変わるかも知れない。 | ||
| 11行目: | 13行目: | ||
関数 $$f(x)$$ に対して | 関数 $$f(x)$$ に対して | ||
| − | :$$\displaystyle{\ | + | :$$\displaystyle{\Delta f(x)=f(x+1)-f(x)}$$ |
| + | |||
| + | なる $$\Delta f(x)$$ を $$f(x)$$ の'''差分'''と呼ぶ。 | ||
| + | |||
| + | これは高校数学では階差数列と呼ばれるものである。 | ||
| − | + | なお微分積分学では | |
| − | + | :$$\displaystyle{\frac d{dx}f(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}h}$$ | |
| − | + | なる $$\frac d{dx}f(x)$$ を $$f(x)$$ の微分と呼ぶ。 | |
| − | + | ここで $$h\to0$$ という極限を取るのではなく $$h=1$$ と固定したものが差分であるという見方もできる。 | |
| − | |||
| − | |||
| − | + | また、差分は微分と同様に $$f(x)$$ の定数項は $$\Delta f(x)$$ に関係がないことは微分よりも明確にわかる。 | |
==積分法と和分法== | ==積分法と和分法== | ||
| 29行目: | 33行目: | ||
:[[File:Piecewise quadrature.png|400px]] | :[[File:Piecewise quadrature.png|400px]] | ||
| − | :$$\displaystyle{\sum\nolimits_a^bf(x)=\sum_{x=a}^{b-1}f(x)}$$ | + | :$$\displaystyle{\sum\nolimits_a^bf(x)\,\delta x=\sum_{x=a}^{b-1}f(x)}$$ |
| − | で表される $$\sum\nolimits_a^bf(x)$$ を $$f(x)$$ の $$a$$ から $$b$$ までの'''定和分'''と呼び、上図の灰色の部分の面積を表す。 | + | で表される $$\sum\nolimits_a^bf(x)\,\delta x$$ を $$f(x)$$ の $$a$$ から $$b$$ までの'''定和分'''と呼び、上図の灰色の部分の面積を表す。 |
なお、終点 $$b$$ は含まれないことに注意する。 | なお、終点 $$b$$ は含まれないことに注意する。 | ||
| 41行目: | 45行目: | ||
===不定積分と不定和分=== | ===不定積分と不定和分=== | ||
| − | + | 差分の逆演算をしたもの、すなわち | |
| + | |||
| + | :$$\displaystyle{\Delta \sum f(x)\,\delta x=f(x)}$$ | ||
| + | |||
| + | を満たす $$\sum f(x)\,\delta x$$ を $$f(x)$$ の'''不定和分'''と呼ぶ。 | ||
| + | |||
| + | 上述の通り差分は元の関数の定数項に関係ないため、不定和分は不定積分と同様に和分定数が生じる。 | ||
| + | <ref group="注">和分定数は定数だけでなく周期が $$\frac1n$$ の周期関数も含まれる。</ref> | ||
| + | |||
| + | なお微分積分学では微分の逆演算をしたもの、すなわち | ||
:$$\displaystyle{\frac d{dx}\int f(x)\,dx=f(x)}$$ | :$$\displaystyle{\frac d{dx}\int f(x)\,dx=f(x)}$$ | ||
| − | を満たす $$\int f(x)\,dx$$ を $$f(x)$$ | + | を満たす $$\int f(x)\,dx$$ を $$f(x)$$ の不定積分と呼ぶ。 |
| + | |||
| + | ==和分差分学の基本定理== | ||
| − | :$$\displaystyle{\Delta \sum f(x)=f(x)}$$ | + | :$$\displaystyle{\begin{align*} |
| + | \Delta\sum\nolimits_a^xf(t)\,\delta t | ||
| + | &=\Delta\sum_{n=a}^{x-1}f(n)\\ | ||
| + | &=\sum_{n=a}^{x}f(n)-\sum_{n=a}^{x-1}f(n)\\ | ||
| + | &=\{f(x)+f(x-1)+\cdots+f(a)\}-\{f(x-1)+f(x-2)+\cdots+f(a)\}\\ | ||
| + | &=f(x) | ||
| + | \end{align*}}$$ | ||
| − | + | より | |
| − | + | :$$\displaystyle{\Delta\sum\nolimits_a^xf(t)\,\delta t=f(x)}$$ | |
| − | + | ||
| + | となる。 | ||
| + | |||
| + | また、$$F(x)=\sum f(x)\,\delta x$$ とした時、上で示した式と前節の不定和分の定義より | ||
| − | + | :$$\displaystyle{F(x)=\sum\nolimits_a^xf(t)\,\delta t+C}$$ | |
| − | :$$\displaystyle{ | ||
| − | + | となり、 | |
| − | :$$\displaystyle{\sum\nolimits_a^bf(t)=F(b)-F(a)}$$ | + | :$$\displaystyle{\sum\nolimits_a^bf(t)\,\delta t=F(b)-F(a)}$$ |
| − | + | が成立する。前節のグラフを見ても明らかである。 | |
| − | + | これらは微分積分学の基本定理に対応する。 | |
==和分差分の性質== | ==和分差分の性質== | ||
| 69行目: | 92行目: | ||
:$$\displaystyle{\Delta kf(x)=k\Delta f(x)}$$ | :$$\displaystyle{\Delta kf(x)=k\Delta f(x)}$$ | ||
:$$\displaystyle{\Delta\{f(x)+g(x)\}=\Delta f(x)+\Delta g(x)}$$ | :$$\displaystyle{\Delta\{f(x)+g(x)\}=\Delta f(x)+\Delta g(x)}$$ | ||
| − | :$$\displaystyle{\sum kf(x)\delta x=k\sum f(x)}$$ | + | :$$\displaystyle{\sum kf(x)\,\delta x=k\sum f(x)\,\delta}$$ |
| − | :$$\displaystyle{\sum \{f(x)+g(x)\}\delta x=\sum f(x)+\sum g(x)}$$ | + | :$$\displaystyle{\sum \{f(x)+g(x)\}\,\delta x=\sum f(x)\,\delta x+\sum g(x)\,\delta x}$$ |
===下降階乗=== | ===下降階乗=== | ||
| − | + | 正の整数 $$n$$ に対して下降階乗 $$x^{\underline n}$$ を | |
:$$x^{\underline n}=x(x-1)(x-2)\cdots(x-n+1)$$ | :$$x^{\underline n}=x(x-1)(x-2)\cdots(x-n+1)$$ | ||
と定義する。 | と定義する。 | ||
| + | |||
| + | 差分をとると | ||
:$$\begin{align*} | :$$\begin{align*} | ||
| − | \Delta x^{\underline n}&=(x+1)x(x-1)(x-2)\cdots(x-n+2)-x(x-1)(x-2)\cdots(x-n+1)\\ | + | \Delta x^{\underline n} |
| + | &=(x+1)x(x-1)(x-2)\cdots(x-n+2)-x(x-1)(x-2)\cdots(x-n+1)\\ | ||
&=\{(x+1)-(x-n+1)\}x(x-1)(x-2)\cdots(x-n+2)\\ | &=\{(x+1)-(x-n+1)\}x(x-1)(x-2)\cdots(x-n+2)\\ | ||
&=nx^{\underline{n-1}} | &=nx^{\underline{n-1}} | ||
\end{align*}$$ | \end{align*}$$ | ||
| − | + | となり、和分差分学の基本定理より | |
| − | :$$\sum x^{\underline n}=\ | + | :$$\displaystyle{\sum x^{\underline n}\,\delta x=\frac{x^{\underline{n+1}}}{n+1}}+C$$ |
が従う。 | が従う。 | ||
| − | + | <ref group="注">下降階乗は整数全体にも拡張できる。ただし上式が成立するのは $$n\neq -1$$ であることに注意する。</ref> | |
これは $$x^n$$ の微分積分に対応する。 | これは $$x^n$$ の微分積分に対応する。 | ||
またこの性質を用いると、 | またこの性質を用いると、 | ||
:$$\displaystyle{\begin{align*} | :$$\displaystyle{\begin{align*} | ||
| − | \sum_{x=1}^nx^2&=\sum\nolimits_1^{n+1}x^2\\ | + | \sum_{x=1}^nx^2 |
| − | &=\sum\nolimits_1^{n+1}\{x(x-1)+x\}\\ | + | &=\sum\nolimits_1^{n+1}x^2\,\delta x\\ |
| − | &=\sum\nolimits_1^{n+1}\{x^{\underline2}+x^{\underline1}\}\\ | + | &=\sum\nolimits_1^{n+1}\{x(x-1)+x\}\,\delta x\\ |
| + | &=\sum\nolimits_1^{n+1}\{x^{\underline2}+x^{\underline1}\}\,\delta x\\ | ||
&=\left[\frac{x^{\underline3}}3+\frac{x^{\underline2}}2\right]_1^{n+1}\\ | &=\left[\frac{x^{\underline3}}3+\frac{x^{\underline2}}2\right]_1^{n+1}\\ | ||
&=\frac16n(n+1)(2n+1) | &=\frac16n(n+1)(2n+1) | ||
\end{align*}}$$ | \end{align*}}$$ | ||
など $$n$$ 乗の和の公式を導くことができる。 | など $$n$$ 乗の和の公式を導くことができる。 | ||
| + | |||
| + | ===指数関数(等比数列)=== | ||
| + | 指数関数$a^x$の差分は | ||
| + | |||
| + | :$$\begin{align*} | ||
| + | \Delta a^x&=a^{x+1}-a^x\\ | ||
| + | &=(a-1)a^x | ||
| + | \end{align*}$$ | ||
| + | |||
| + | となるので、両辺和分をとって整理すると$a\ne1$のとき | ||
| + | |||
| + | :$$\displaystyle\sum a^x\delta=\frac{a^x}{a-1}$$ | ||
| + | |||
| + | となる。 | ||
| + | |||
| + | 高校数学で見慣れた等比数列の和の公式もここから導出できる。 | ||
| + | |||
| + | :$$\begin{align*} | ||
| + | \sum_{k=1}^nar^{k-1}&=\sum\nolimits_1^{n+1}ar^{x-1}\,\delta x\\ | ||
| + | &=\left[a\frac{r^{x-1}}{r-1}\right]_1^{n+1}\\ | ||
| + | &=a\frac{r^n}{r-1}-a\frac{1}{r-1}\\ | ||
| + | &=a\frac{r^n-1}{r-1} | ||
| + | \end{align*}$$ | ||
| + | |||
| + | ===積の差分と部分和分=== | ||
| + | 積の微分に対して積の差分は | ||
| + | :$$\displaystyle{\begin{align*} | ||
| + | \Delta\{f(x)g(x)\} | ||
| + | &=f(x+1)g(x+1)-f(x)g(x)\\ | ||
| + | &=f(x)g(x+1)-f(x)g(x)+f(x+1)g(x+1)-f(x)g(x+1)\\ | ||
| + | &=f(x)\Delta g(x)+g(x+1)\Delta f(x) | ||
| + | \end{align*}}$$ | ||
| + | となり、両辺を和分し整理することによって部分和分 | ||
| + | :$$\displaystyle{\sum f(x)\Delta g(x)\,\delta x=f(x)g(x)-\sum g(x+1)\Delta f(x)\,\delta x}$$ | ||
| + | :$$\displaystyle{\sum\nolimits_a^b f(x)\Delta g(x)\,\delta x=\left[f(x)g(x)\right]_a^b-\sum\nolimits_a^b g(x+1)\Delta f(x)\,\delta x}$$ | ||
| + | を導ける。 | ||
| + | |||
| + | 実際に積の和分を使用して高校数学でお馴染みの和を求めてみる。 | ||
| + | |||
| + | :$$\begin{align*} | ||
| + | \sum_{k=1}^nk2^k&=\sum\nolimits_1^{n+1} x2^x\,\delta x\\ | ||
| + | &=\sum\nolimits_1^{n+1} x\Delta2^x\,\delta x\\ | ||
| + | &=\left[x2^x\right]_1^{n+1}-\sum\nolimits_1^{n+1} 2^{x+1}\Delta x\,\delta x\\ | ||
| + | &=(n+1)2^{n+1}-2-\sum\nolimits_1^{n+1} 2^{x+1}\,\delta x\\ | ||
| + | &=(n+1)2^{n+1}-2-[2^{x+1}]_1^{n+1}\\ | ||
| + | &=(n+1)2^{n+1}-2-(2^{n+2}-4)\\ | ||
| + | &=(n-1)2^{n+1}+2 | ||
| + | \end{align*}$$ | ||
==注== | ==注== | ||
<references group="注"/> | <references group="注"/> | ||
2020年11月29日 (日) 11:32時点における最新版
この記事は主に高校数学においての数列と微分積分法の分野の関係についての独自研究である。
なお、この記事は編集中である。
目次
はじめに
高校数学では数列と関数は全くの別物のように扱われているが、数列も主に自然数に対して定義されている歴とした関数である。
そのためここでは微分積分学との関係がわかりやすくなるよう数列を $$a_n$$ といった表記ではなく $$f(x)$$ という表記にする。
極限を扱う微分積分よりも以下に述べる和分差分は直感的に分かりやすい為、数列だけでなく微分積分の見方も変わるかも知れない。
微分法と差分法
関数 $$f(x)$$ に対して
- $$\displaystyle{\Delta f(x)=f(x+1)-f(x)}$$
なる $$\Delta f(x)$$ を $$f(x)$$ の差分と呼ぶ。
これは高校数学では階差数列と呼ばれるものである。
なお微分積分学では
- $$\displaystyle{\frac d{dx}f(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}h}$$
なる $$\frac d{dx}f(x)$$ を $$f(x)$$ の微分と呼ぶ。
ここで $$h\to0$$ という極限を取るのではなく $$h=1$$ と固定したものが差分であるという見方もできる。
また、差分は微分と同様に $$f(x)$$ の定数項は $$\Delta f(x)$$ に関係がないことは微分よりも明確にわかる。
積分法と和分法
定積分と定和分
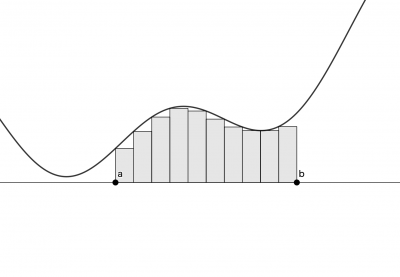
- $$\displaystyle{\sum\nolimits_a^bf(x)\,\delta x=\sum_{x=a}^{b-1}f(x)}$$
で表される $$\sum\nolimits_a^bf(x)\,\delta x$$ を $$f(x)$$ の $$a$$ から $$b$$ までの定和分と呼び、上図の灰色の部分の面積を表す。 なお、終点 $$b$$ は含まれないことに注意する。
この時上図の長方形の横幅はそれぞれ $$1$$ であるが、この幅の $$0$$ への極限をとった時の面積が
- $$\displaystyle{\int_a^bf(x)\,dx}$$
であり、 $$f(x)$$ の $$a$$ から $$b$$ までの定積分である。
不定積分と不定和分
差分の逆演算をしたもの、すなわち
- $$\displaystyle{\Delta \sum f(x)\,\delta x=f(x)}$$
を満たす $$\sum f(x)\,\delta x$$ を $$f(x)$$ の不定和分と呼ぶ。
上述の通り差分は元の関数の定数項に関係ないため、不定和分は不定積分と同様に和分定数が生じる。 [注 1]
なお微分積分学では微分の逆演算をしたもの、すなわち
- $$\displaystyle{\frac d{dx}\int f(x)\,dx=f(x)}$$
を満たす $$\int f(x)\,dx$$ を $$f(x)$$ の不定積分と呼ぶ。
和分差分学の基本定理
- $$\displaystyle{\begin{align*} \Delta\sum\nolimits_a^xf(t)\,\delta t &=\Delta\sum_{n=a}^{x-1}f(n)\\ &=\sum_{n=a}^{x}f(n)-\sum_{n=a}^{x-1}f(n)\\ &=\{f(x)+f(x-1)+\cdots+f(a)\}-\{f(x-1)+f(x-2)+\cdots+f(a)\}\\ &=f(x) \end{align*}}$$
より
- $$\displaystyle{\Delta\sum\nolimits_a^xf(t)\,\delta t=f(x)}$$
となる。
また、$$F(x)=\sum f(x)\,\delta x$$ とした時、上で示した式と前節の不定和分の定義より
- $$\displaystyle{F(x)=\sum\nolimits_a^xf(t)\,\delta t+C}$$
となり、
- $$\displaystyle{\sum\nolimits_a^bf(t)\,\delta t=F(b)-F(a)}$$
が成立する。前節のグラフを見ても明らかである。
これらは微分積分学の基本定理に対応する。
和分差分の性質
線形性
- $$\displaystyle{\Delta kf(x)=k\Delta f(x)}$$
- $$\displaystyle{\Delta\{f(x)+g(x)\}=\Delta f(x)+\Delta g(x)}$$
- $$\displaystyle{\sum kf(x)\,\delta x=k\sum f(x)\,\delta}$$
- $$\displaystyle{\sum \{f(x)+g(x)\}\,\delta x=\sum f(x)\,\delta x+\sum g(x)\,\delta x}$$
下降階乗
正の整数 $$n$$ に対して下降階乗 $$x^{\underline n}$$ を
- $$x^{\underline n}=x(x-1)(x-2)\cdots(x-n+1)$$
と定義する。
差分をとると
- $$\begin{align*} \Delta x^{\underline n} &=(x+1)x(x-1)(x-2)\cdots(x-n+2)-x(x-1)(x-2)\cdots(x-n+1)\\ &=\{(x+1)-(x-n+1)\}x(x-1)(x-2)\cdots(x-n+2)\\ &=nx^{\underline{n-1}} \end{align*}$$
となり、和分差分学の基本定理より
- $$\displaystyle{\sum x^{\underline n}\,\delta x=\frac{x^{\underline{n+1}}}{n+1}}+C$$
が従う。 [注 2] これは $$x^n$$ の微分積分に対応する。
またこの性質を用いると、
- $$\displaystyle{\begin{align*} \sum_{x=1}^nx^2 &=\sum\nolimits_1^{n+1}x^2\,\delta x\\ &=\sum\nolimits_1^{n+1}\{x(x-1)+x\}\,\delta x\\ &=\sum\nolimits_1^{n+1}\{x^{\underline2}+x^{\underline1}\}\,\delta x\\ &=\left[\frac{x^{\underline3}}3+\frac{x^{\underline2}}2\right]_1^{n+1}\\ &=\frac16n(n+1)(2n+1) \end{align*}}$$
など $$n$$ 乗の和の公式を導くことができる。
指数関数(等比数列)
指数関数$a^x$の差分は
- $$\begin{align*} \Delta a^x&=a^{x+1}-a^x\\ &=(a-1)a^x \end{align*}$$
となるので、両辺和分をとって整理すると$a\ne1$のとき
- $$\displaystyle\sum a^x\delta=\frac{a^x}{a-1}$$
となる。
高校数学で見慣れた等比数列の和の公式もここから導出できる。
- $$\begin{align*} \sum_{k=1}^nar^{k-1}&=\sum\nolimits_1^{n+1}ar^{x-1}\,\delta x\\ &=\left[a\frac{r^{x-1}}{r-1}\right]_1^{n+1}\\ &=a\frac{r^n}{r-1}-a\frac{1}{r-1}\\ &=a\frac{r^n-1}{r-1} \end{align*}$$
積の差分と部分和分
積の微分に対して積の差分は
- $$\displaystyle{\begin{align*} \Delta\{f(x)g(x)\} &=f(x+1)g(x+1)-f(x)g(x)\\ &=f(x)g(x+1)-f(x)g(x)+f(x+1)g(x+1)-f(x)g(x+1)\\ &=f(x)\Delta g(x)+g(x+1)\Delta f(x) \end{align*}}$$
となり、両辺を和分し整理することによって部分和分
- $$\displaystyle{\sum f(x)\Delta g(x)\,\delta x=f(x)g(x)-\sum g(x+1)\Delta f(x)\,\delta x}$$
- $$\displaystyle{\sum\nolimits_a^b f(x)\Delta g(x)\,\delta x=\left[f(x)g(x)\right]_a^b-\sum\nolimits_a^b g(x+1)\Delta f(x)\,\delta x}$$
を導ける。
実際に積の和分を使用して高校数学でお馴染みの和を求めてみる。
- $$\begin{align*} \sum_{k=1}^nk2^k&=\sum\nolimits_1^{n+1} x2^x\,\delta x\\ &=\sum\nolimits_1^{n+1} x\Delta2^x\,\delta x\\ &=\left[x2^x\right]_1^{n+1}-\sum\nolimits_1^{n+1} 2^{x+1}\Delta x\,\delta x\\ &=(n+1)2^{n+1}-2-\sum\nolimits_1^{n+1} 2^{x+1}\,\delta x\\ &=(n+1)2^{n+1}-2-[2^{x+1}]_1^{n+1}\\ &=(n+1)2^{n+1}-2-(2^{n+2}-4)\\ &=(n-1)2^{n+1}+2 \end{align*}$$