「ガラパゴ三辺比定理」の版間の差分
| (同じ利用者による、間の47版が非表示) | |||
| 1行目: | 1行目: | ||
| − | ''' | + | '''ガラパゴ三辺比定理'''(ガラパゴさんぺんひていり)とは、ユークリッド平面上の三角形 $$\triangle OAB$$ において、長さが $$x$$ の辺 $$OA$$ と 長さが $$y$$ の辺 $$AB$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、辺 $$OB$$ を $$O$$ を中心として $$\angle O$$ の偶数倍回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表せるという定理である。 |
| + | |||
| + | [[ガラパゴ数学]]の主定理の一つで、[[みゆ]] により考案された。特に $$\theta=\frac{\pi}{2}~\mathrm{rad}$$ の場合は'''ピタゴラスの定理II'''、'''ピタツー'''などの愛称で呼ばれることもあり、整数の性質を扱うときは主にそちらが用いられる。 | ||
| + | |||
==概要== | ==概要== | ||
| − | $$\theta~\mathrm{rad}$$ | + | 辺 $$OA$$ の長さが $$x$$、辺 $$AB$$ の長さが $$y$$、これら二辺の成す内角が $$\angle A=\theta~\mathrm{rad}$$ であるようなユークリッド平面上の三角形 $$\triangle OAB$$ の三辺比は次の通りである。 |
| + | |||
| + | |||
| + | :$$x$$ : $$y$$ : $$\sqrt{x^2+y^2-2xy\cos\theta}$$ | ||
| + | |||
| + | |||
| + | この三辺比は、$$OA$$ 上に $$\angle OA'B$$ が直角となるような点 $$A'$$ を置くことで(その直角を挟む二辺の長さがそれぞれ $$x+y\cos(\pi-\theta)$$ と $$y\sin(\pi-\theta)$$ であることから)容易に導出できるが、三平方の定理に起因する平方根項が存在するため整式の比とはなっていない。 | ||
| + | |||
| + | しかし、$$\angle O$$ を偶数倍すなわち辺 $$OB$$ を $$O$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表すことができる。 | ||
| − | |||
| − | + | $$\angle O$$ を2倍した場合 | |
| + | |||
| + | :$$x^2-y^2$$ : $$2xy-ry^2$$ : $$x^2+y^2-rxy$$ | ||
| + | |||
| + | |||
| + | $$\angle O$$ を4倍した場合 | ||
| + | |||
| + | :$$x^4+y^4-6x^2y^2+4rxy^3-r^2y^4$$ : $$4x^3y+6rx^2y^2-4xy^3+4r^2xy^3-2ry^4+r^3y^4$$ : $$(x^2+y^2-rxy)^2$$ | ||
| + | |||
| + | |||
| + | このとき、三辺比の第一項と第二項に対応する二辺の成す角の角度が $$\theta~\mathrm{rad}$$ となる。ここでいう二辺の成す角とは必ずしも三角形の内角を指すものではない。辺 $$OA$$ と辺 $$AB$$ の伸縮によっていずれか一方のみが負数倍となる場合、三角形としては内角と外角が入れ替わるため、その場合は外角が $$\theta~\mathrm{rad}$$ であり内角は $$\pi-\theta~\mathrm{rad}$$ となる。 | ||
| + | |||
| + | 角度を2倍することの意味は、平方根項に対応する辺 $$OB$$ の長さを $$1$$ として相似比 $$1$$:$$OB$$ の相似三角形を作る([[ガラパゴ数学]]の乗算の項を参照)ことにある。その結果、$$OB$$ に対応する辺の長さも $$1$$:$$OB=OB$$:$$OB^2$$ となり、結果として $$OB$$ の二乗が作り出されて根号が外れている。同様に角度を偶数倍すれば相似比も偶数乗倍となり根号を外すことができる。 | ||
==導出== | ==導出== | ||
| 12行目: | 34行目: | ||
角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、 | 角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、 | ||
| + | |||
| + | |||
:$$x$$ : $$y$$ : $$|x+yz|$$ | :$$x$$ : $$y$$ : $$|x+yz|$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | である。この三角形の第三項 $$|x+yz|$$ に対応する辺を第一項 $$x$$ に対応する辺との狭角が2倍になるように回転して延長したとき、これによって得られた直線は $$(x+yz)$$ を $$+1$$ とみなした相似な座標系においても同じく $$x+yz$$ を通る。 | |
| − | \ | + | |
| − | (x+yz)^2= | + | すなわちこの基底空間上の座標において、この直線は |
| − | =&x^2+y^2( | + | |
| − | =&(x^2-y^2)+(2xy | + | |
| − | \end{align} | + | :$$(x+yz)\times(x+yz)=(x+yz)^2=x^2+y^2z^2+2xyz$$ |
| − | + | ||
| + | |||
| + | を通るといえる。([[ガラパゴ数学]]の乗算の項を参照) | ||
| + | |||
| + | この座標は[[ガラパゴ累乗定理]]により $$1$$ と $$z$$ の一次結合の形で表すことができる。 | ||
| + | |||
| + | |||
| + | :$$r'=2\cos(\pi-\theta)=-2\cos\theta$$ | ||
| + | :$$z^2=r'z-1$$ | ||
| + | |||
| + | |||
| + | :$$\begin{align*} | ||
| + | (x+yz)^2=&x^2+y^2(r'z-1)+2xyz\\ | ||
| + | =&(x^2-y^2)+(2xy+r'y^2)z\\ | ||
| + | \end{align*}$$ | ||
| + | |||
| + | |||
| + | これを新たな三角形とみるならばその三辺比は | ||
| + | |||
| + | |||
| + | :$$x^2-y^2$$ : $$2xy+r'y^2$$ : $$|x+yz|^2$$ | ||
| + | |||
| + | |||
| + | すなわち | ||
| + | |||
| + | |||
:$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$ | :$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$ | ||
| − | + | ||
| + | |||
| + | となっており、さらに $$z=e^{i(\pi-\theta)}=\cos(\pi-\theta)+i\sin(\pi-\theta)$$ と展開すれば | ||
| + | |||
| + | |||
| + | :$$\begin{align*} | ||
| + | |x+yz|^2=&\big|[x+y\cos(\pi-\theta)]+[y\sin(\pi-\theta)]i\big|^2\\ | ||
| + | =&\left(\sqrt{[x+y\cos(\pi-\theta)]^2+[y\sin(\pi-\theta)]^2}\right)^2\\ | ||
| + | =&\left(\sqrt{(x-y\cos\theta)^2+(y\sin\theta)^2}\right)^2\\ | ||
| + | =&\left(\sqrt{x^2+y^2(\cos^2\theta+\sin^2\theta)-2xy\cos\theta}\right)^2\\ | ||
| + | =&\left(\sqrt{x^2+y^2-2xy\cos\theta}\right)^2\\ | ||
| + | =&x^2+y^2-2xy\cos\theta | ||
| + | |||
| + | \end{align*}$$ | ||
| + | |||
| + | |||
| + | であるため、したがって先程の比率は | ||
| + | |||
| + | |||
:$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$ | :$$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$ | ||
| − | |||
| − | + | または $$r=2\cos\theta$$ を用いて | |
| − | |||
| − | |||
| − | :$$(x^2+y^2-2xy\cos\theta)^2=(x^2-y^2)^2+(2xy-2y^2\cos\theta)^2-2(x^2-y^2)(2xy-2y^2\cos\theta)\cos\theta | + | :$$x^2-y^2$$ : $$2xy-ry^2$$ : $$x^2+y^2-rxy$$ |
| + | |||
| + | |||
| + | と書き改めることができる。この三角形は $$1$$ と $$z$$ を基底とする斜交座標形式の複素数で表されていることから二辺の成す角は $$\theta~\mathrm{rad}$$ であり、したがって、この比率で作られた三角形は二辺の成す角が $$\theta~\mathrm{rad}$$ といえる。 | ||
| + | |||
| + | |||
| + | [[ファイル:ガラパゴ三辺比定理.png]] | ||
| + | |||
| + | |||
| + | この操作で狭角を2倍ではなく一般に偶数倍として回転させた場合でも、相似比は偶数乗を想定することになるため $$|x+yz|=\sqrt{x^2+y^2-2xy\cos\theta}$$ は偶数乗されて根号が外れる。 | ||
| + | |||
| + | ==三辺比恒等式== | ||
| + | ガラパゴ三辺比定理で示される三角形の三辺比より、以下の恒等式を導くことができる。 | ||
| + | |||
| + | \begin{align*} | ||
| + | &(x^2+y^2-2xy\cos\theta)^2\\ | ||
| + | =&\big|(x^2-y^2)+(2xy-2y^2\cos\theta)e^{i(\pi-\theta)}\big|^2\\ | ||
| + | =&(x^2-y^2)^2+(2xy-2y^2\cos\theta)^2-2(x^2-y^2)(2xy-2y^2\cos\theta)\cos\theta | ||
| + | \end{align*} | ||
==拡張ピタゴラス数== | ==拡張ピタゴラス数== | ||
| − | $$\cos\theta$$ | + | 二辺の成す角 $$θ$$ において $$\cos\theta$$ が有理数値であるような三角形の三辺比は、ガラパゴ三辺比定理を用いると整数比で表すことができる。このような整数比を'''拡張ピタゴラス比'''、その整数の組を'''拡張ピタゴラス数'''と呼ぶ。これは直角三角形の三辺を整数比とするピタゴラス数の純粋な拡張となっていることに由来する。 |
| + | |||
| + | ここで、三角形の二辺の成す角が必ずしも三角形の内角とは限らないことに注意が必要である。三角形としてみた場合、辺の長さが負の値をとると内角と外角が入れ替わり、そのようなケースでは外角が $$\theta~\mathrm{rad}$$、内角が $$\pi-\theta~\mathrm{rad}$$ となる。 | ||
| + | |||
| + | |||
| + | 二辺の成す角が $$\theta=~\frac{\pi}{3}~\mathrm{rad}~(60^{\circ})$$ である三角形の三辺比 | ||
| + | :$$x^2-y^2$$ : $$2xy-y^2$$ : $$x^2+y^2-xy$$ | ||
| + | [[ファイル:拡張ピタゴラス数60.png]] | ||
| − | + | 二辺の成す角が $$\theta=~\frac{\pi}{2}~\mathrm{rad}~(90^{\circ})$$ である三角形の三辺比 | |
:$$x^2-y^2$$ : $$2xy$$ : $$x^2+y^2$$ | :$$x^2-y^2$$ : $$2xy$$ : $$x^2+y^2$$ | ||
| − | + | [[ファイル:拡張ピタゴラス数90.png]] | |
| − | : | ||
| − | |||
| − | |||
| − | + | 二辺の成す角が $$\theta=~\frac{2\pi}{3}~\mathrm{rad}~(120^{\circ})$$ である三角形の三辺比 | |
| + | :$$x^2-y^2$$ : $$2xy+y^2$$ : $$x^2+y^2+xy$$ | ||
| + | [[ファイル:拡張ピタゴラス数120.png]] | ||
2020年2月2日 (日) 08:31時点における最新版
ガラパゴ三辺比定理(ガラパゴさんぺんひていり)とは、ユークリッド平面上の三角形 $$\triangle OAB$$ において、長さが $$x$$ の辺 $$OA$$ と 長さが $$y$$ の辺 $$AB$$ の成す内角が $$\angle A=\theta~\mathrm{rad}$$ である場合、辺 $$OB$$ を $$O$$ を中心として $$\angle O$$ の偶数倍回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表せるという定理である。
ガラパゴ数学の主定理の一つで、みゆ により考案された。特に $$\theta=\frac{\pi}{2}~\mathrm{rad}$$ の場合はピタゴラスの定理II、ピタツーなどの愛称で呼ばれることもあり、整数の性質を扱うときは主にそちらが用いられる。
概要
辺 $$OA$$ の長さが $$x$$、辺 $$AB$$ の長さが $$y$$、これら二辺の成す内角が $$\angle A=\theta~\mathrm{rad}$$ であるようなユークリッド平面上の三角形 $$\triangle OAB$$ の三辺比は次の通りである。
- $$x$$ : $$y$$ : $$\sqrt{x^2+y^2-2xy\cos\theta}$$
この三辺比は、$$OA$$ 上に $$\angle OA'B$$ が直角となるような点 $$A'$$ を置くことで(その直角を挟む二辺の長さがそれぞれ $$x+y\cos(\pi-\theta)$$ と $$y\sin(\pi-\theta)$$ であることから)容易に導出できるが、三平方の定理に起因する平方根項が存在するため整式の比とはなっていない。
しかし、$$\angle O$$ を偶数倍すなわち辺 $$OB$$ を $$O$$ を中心として回転させ、それに伴って各辺の長さを伸縮(負数倍も可)して得られる新たな三角形の三辺比は $$x$$、$$y$$、$$r=2\cos\theta$$ の整式で表すことができる。
$$\angle O$$ を2倍した場合
- $$x^2-y^2$$ : $$2xy-ry^2$$ : $$x^2+y^2-rxy$$
$$\angle O$$ を4倍した場合
- $$x^4+y^4-6x^2y^2+4rxy^3-r^2y^4$$ : $$4x^3y+6rx^2y^2-4xy^3+4r^2xy^3-2ry^4+r^3y^4$$ : $$(x^2+y^2-rxy)^2$$
このとき、三辺比の第一項と第二項に対応する二辺の成す角の角度が $$\theta~\mathrm{rad}$$ となる。ここでいう二辺の成す角とは必ずしも三角形の内角を指すものではない。辺 $$OA$$ と辺 $$AB$$ の伸縮によっていずれか一方のみが負数倍となる場合、三角形としては内角と外角が入れ替わるため、その場合は外角が $$\theta~\mathrm{rad}$$ であり内角は $$\pi-\theta~\mathrm{rad}$$ となる。
角度を2倍することの意味は、平方根項に対応する辺 $$OB$$ の長さを $$1$$ として相似比 $$1$$:$$OB$$ の相似三角形を作る(ガラパゴ数学の乗算の項を参照)ことにある。その結果、$$OB$$ に対応する辺の長さも $$1$$:$$OB=OB$$:$$OB^2$$ となり、結果として $$OB$$ の二乗が作り出されて根号が外れている。同様に角度を偶数倍すれば相似比も偶数乗倍となり根号を外すことができる。
導出
$$+1$$ と $$z=e^{i(\pi-\theta)}$$ を元とする基底空間において、内角の一つに $$\theta~\mathrm{rad}$$ をもつ三角形を想定する。
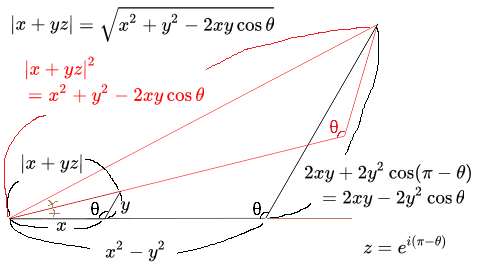
角度が $$\theta~\mathrm{rad}$$ である内角の対辺を $$x+yz$$ で表現すると、ここに見いだされる三角形の三辺比は、
- $$x$$ : $$y$$ : $$|x+yz|$$
である。この三角形の第三項 $$|x+yz|$$ に対応する辺を第一項 $$x$$ に対応する辺との狭角が2倍になるように回転して延長したとき、これによって得られた直線は $$(x+yz)$$ を $$+1$$ とみなした相似な座標系においても同じく $$x+yz$$ を通る。
すなわちこの基底空間上の座標において、この直線は
- $$(x+yz)\times(x+yz)=(x+yz)^2=x^2+y^2z^2+2xyz$$
を通るといえる。(ガラパゴ数学の乗算の項を参照)
この座標はガラパゴ累乗定理により $$1$$ と $$z$$ の一次結合の形で表すことができる。
- $$r'=2\cos(\pi-\theta)=-2\cos\theta$$
- $$z^2=r'z-1$$
- $$\begin{align*} (x+yz)^2=&x^2+y^2(r'z-1)+2xyz\\ =&(x^2-y^2)+(2xy+r'y^2)z\\ \end{align*}$$
これを新たな三角形とみるならばその三辺比は
- $$x^2-y^2$$ : $$2xy+r'y^2$$ : $$|x+yz|^2$$
すなわち
- $$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$|x+yz|^2$$
となっており、さらに $$z=e^{i(\pi-\theta)}=\cos(\pi-\theta)+i\sin(\pi-\theta)$$ と展開すれば
- $$\begin{align*} |x+yz|^2=&\big|[x+y\cos(\pi-\theta)]+[y\sin(\pi-\theta)]i\big|^2\\ =&\left(\sqrt{[x+y\cos(\pi-\theta)]^2+[y\sin(\pi-\theta)]^2}\right)^2\\ =&\left(\sqrt{(x-y\cos\theta)^2+(y\sin\theta)^2}\right)^2\\ =&\left(\sqrt{x^2+y^2(\cos^2\theta+\sin^2\theta)-2xy\cos\theta}\right)^2\\ =&\left(\sqrt{x^2+y^2-2xy\cos\theta}\right)^2\\ =&x^2+y^2-2xy\cos\theta \end{align*}$$
であるため、したがって先程の比率は
- $$x^2-y^2$$ : $$2xy-2y^2\cos\theta$$ : $$x^2+y^2-2xy\cos\theta$$
または $$r=2\cos\theta$$ を用いて
- $$x^2-y^2$$ : $$2xy-ry^2$$ : $$x^2+y^2-rxy$$
と書き改めることができる。この三角形は $$1$$ と $$z$$ を基底とする斜交座標形式の複素数で表されていることから二辺の成す角は $$\theta~\mathrm{rad}$$ であり、したがって、この比率で作られた三角形は二辺の成す角が $$\theta~\mathrm{rad}$$ といえる。
この操作で狭角を2倍ではなく一般に偶数倍として回転させた場合でも、相似比は偶数乗を想定することになるため $$|x+yz|=\sqrt{x^2+y^2-2xy\cos\theta}$$ は偶数乗されて根号が外れる。
三辺比恒等式
ガラパゴ三辺比定理で示される三角形の三辺比より、以下の恒等式を導くことができる。
\begin{align*} &(x^2+y^2-2xy\cos\theta)^2\\ =&\big|(x^2-y^2)+(2xy-2y^2\cos\theta)e^{i(\pi-\theta)}\big|^2\\ =&(x^2-y^2)^2+(2xy-2y^2\cos\theta)^2-2(x^2-y^2)(2xy-2y^2\cos\theta)\cos\theta \end{align*}
拡張ピタゴラス数
二辺の成す角 $$θ$$ において $$\cos\theta$$ が有理数値であるような三角形の三辺比は、ガラパゴ三辺比定理を用いると整数比で表すことができる。このような整数比を拡張ピタゴラス比、その整数の組を拡張ピタゴラス数と呼ぶ。これは直角三角形の三辺を整数比とするピタゴラス数の純粋な拡張となっていることに由来する。
ここで、三角形の二辺の成す角が必ずしも三角形の内角とは限らないことに注意が必要である。三角形としてみた場合、辺の長さが負の値をとると内角と外角が入れ替わり、そのようなケースでは外角が $$\theta~\mathrm{rad}$$、内角が $$\pi-\theta~\mathrm{rad}$$ となる。
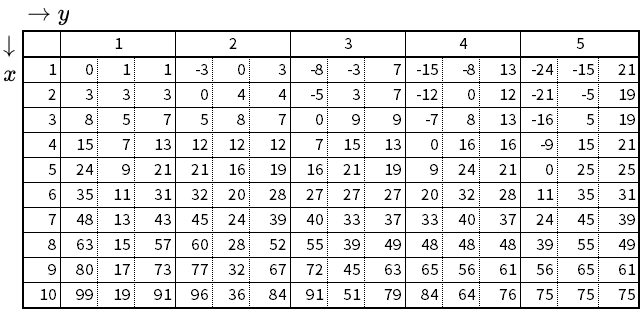
二辺の成す角が $$\theta=~\frac{\pi}{3}~\mathrm{rad}~(60^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy-y^2$$ : $$x^2+y^2-xy$$
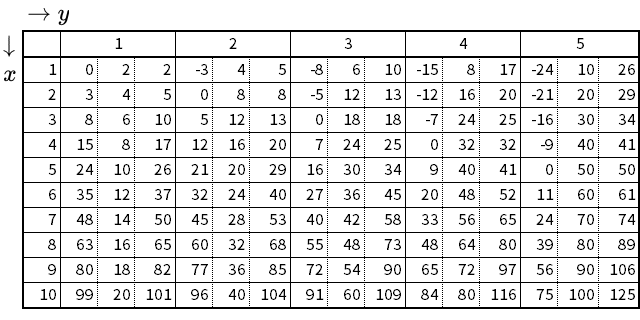
二辺の成す角が $$\theta=~\frac{\pi}{2}~\mathrm{rad}~(90^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy$$ : $$x^2+y^2$$
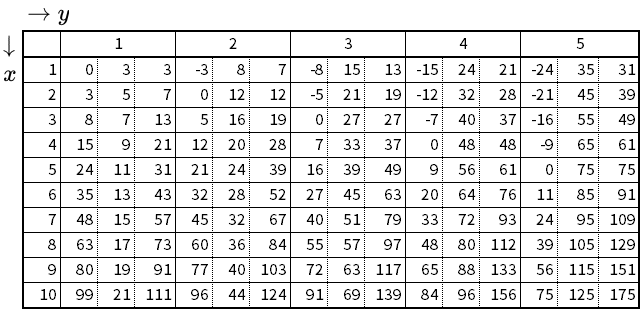
二辺の成す角が $$\theta=~\frac{2\pi}{3}~\mathrm{rad}~(120^{\circ})$$ である三角形の三辺比
- $$x^2-y^2$$ : $$2xy+y^2$$ : $$x^2+y^2+xy$$